Решение. Центр вписанной и описанной окружностей в равнобедренном треугольнике расположены на высоте, поэтому возможны два случая расположения: когда выше центр

Решение

Центр вписанной и описанной окружностей в равнобедренном треугольнике расположены на высоте, поэтому возможны два случая расположения: когда выше центр описанной окружности и когда выше центр вписанной окружности.

1-й случай.

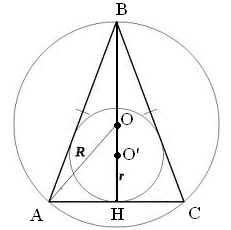
Расстояние между центрами найдем по формуле Эйлера:

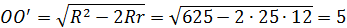
Тогда: 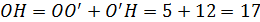. По теореме Пифагора:

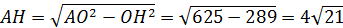
Значит .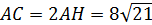

Высота: 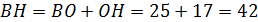. Тогда по теореме Пифагора:

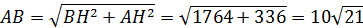
2-й случай.

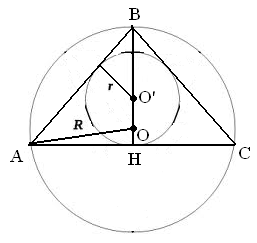
Расстояние между центрами найдем по формуле Эйлера:

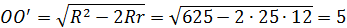
Тогда: 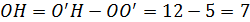. По теореме Пифагора:

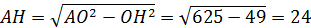
Значит .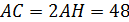

Высота: 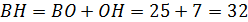. Тогда по теореме Пифагора:

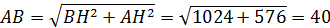
Ответ: 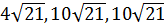или 48, 40, 40.

№2

Найдите радиус окружности, касающейся двух концентрических окружностей радиусов 3 и 5.

Решение

Искомая окружность может касаться обеих окружностей внутренним образом, либо меньшей из данных внешним образом, а большей — внутренним.

1-й случай

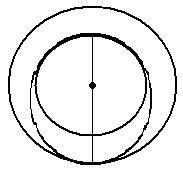
В этом случае:

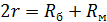
Отсюда:

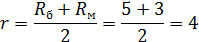
2-й случай

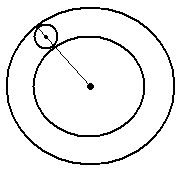
В этом случае:

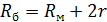
Отсюда:

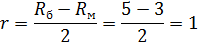
Ответ: 1 или 4.

№3

В треугольник АВС со сторонами AВ = 18 и BC =12 вписан параллелограмм BKLM, причем точки К, L, M лежат на сторонах АВ, АС и ВС соответственно. Известно, что площадь параллелограмма составляет площади треугольника АВС. Найдите стороны параллелограмма.