Оценка согласованности мнений экспертов

Степень согласованности мнений экспертов, как упоминалось выше, влияет на точность результатов проводимой экспертизы. При низкой согласованности мнений экспертов проводится содержательный анализ их оценок с целью выявления причин значительного различия в оценках. Если это объясняется недобросовестностью экспертов, то следует повторить экспертный опрос.

Оценка степени согласованности экспертов может проводиться с помощью различных методов: коэффициента вариации, коэффициента ранговой корреляции Спирмена, коэффициента конкордации и др.

Коэффициент вариации используется при оценках в физических единицах величин, бальных оценках, попарных сравнениях. Он характеризует относительную степень разброса мнений экспертов по отношению к среднему значению коллективной оценки. Степень согласованности мнений экспертов считается удовлетворительной, если коэффициент вариации не превышает значения 0,30 и хорошей когда коэффициент вариации не более 0,20.

Коэффициент ранговой корреляции Спирмена может использоваться для оценки меры близости ранжировок, выполненных двумя экспертами.

При отсутствии одинаковых рангов в ранговом ряду коэффициент ранговой корреляции рассчитывается по формуле:

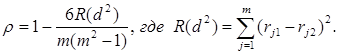(3.21)

Здесь r_j1, r_j2   – ранги, полученные j -м элементом от 1 и 2-го экспертов соответственно; d_j = r_j1 – r_j2 – разности между рангами поставленными экспертами; m – количество ранжируемых элементов.

Чем меньше разности между рангами, тем больше будет r итем ближе его значение будет к + 1,0. Если корреляция отсутствует, то все ранги будут перемешаны и между ними не будет никакого соответствия, тогда значение r окажется близким к 0.

Ограничения по применению коэффициента: количество ранжируемых элементов в каждой выборке должно быть от 5 до 40 (5 £ m £ 40); при большом количестве одинаковых рангов по одной или обеим выборкам коэффициент r дает приближенные значения (идеальным считается вариант, когда оба коррелируемых ряда представлены несовпадающими рангами), поэтому делается поправка на одинаковые ранги.

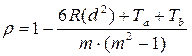, (3.22)

где 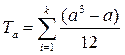, 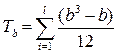- поправки.

Здесь a, b – объемы каждой группы одинаковых рангов в первом и втором ранговом ряду соответственно; k, l – количество групп с одинаковыми рангами в первом и втором ряду.

Для данного m по таблице (см. приложение 1) определяется критичесское значение r_кр. Если рассчитанное значение r ³ r_кр , то корреляционная связь между двумя ранговыми рядами будет достоверна при заданном уровне значимости a.

Пример. 3.11. Два эксперта проранжировали шесть (m = 6) факторов риска (Х₁,Х₂,…,Х₆) по степени их важности. Оценить меру близости ранжировок, выполненных экспертами с помощью коэффициента ранговой корреляции Спирмена при уровне значимости a = 0,05. Исходные данные представлены на рис. 3.18.

Решение

1. Рассчитываются квадраты отклонений d² в оценке по каждому i -му показателю, ячейки В7:G7, рис. 3.18.

2. Вычисляется сумма квадратов по всем отклонениям в оценках экспертов R(d ²), ячейка J5.

3. Определяется фактическое значение коэффициента ранговой корреляции по формуле (3.22), которое равно r = 0,771, ячейка J6.

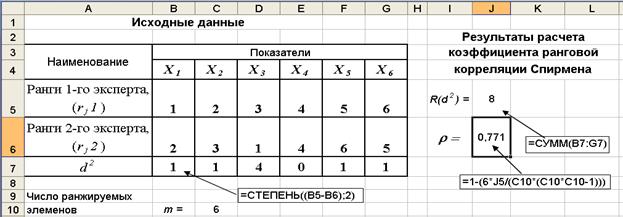
Рис. 3.18. Результаты расчета коэффициента ранговой корреляции Спирмена

4. Рассчитанное значение коэффициента ранговой корреляции сравнивается с критическим значением r_кр = 0,65 - для шести наблюдений (m = 6) и уровня значимости a = 0,05 (см. Приложение 2). Поскольку r ³ r_кр то это означает, что мнения экспертов в оценке шести показателей в основном совпадают и результатам такой экспертизы можно доверять.

Коэффициент конкордации позволяет определитьстепень согласованности мнений экспертов по всем оцениваемым объектам, когда число экспертов более двух.

Коэффициент конкордации рассчитывается по следующей схеме.

1. Вычисляется сумма рангов, полученных j -м элементом от всех экспертов:

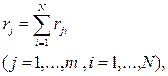(3.23)

где r_{j i} – ранг, полученный j -м элементом от i -го эксперта;

N – количество экспертов, принимающих участие в экспертизе.

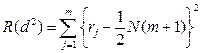
2. Рассчитывается величина R(d ²):

. (3.24)

3. Рассчитывается максимально возможное значение R_m(d ²), для идеального случая, когда ранжировки всех экспертов совпадают:

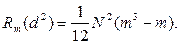(3.25)

4. Вычисляется значение коэффициента конкордации W, какотношение полученного значения R(d ²) к максимально возможному R_m(d ²).

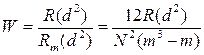(3.26)

Коэффициент конкордации W принимает значения от 0 до 1,0. При W = 1,0 имеет место полная согласованность мнений экспертов, при W > 0,5 – удовлетворительнаяи при W < 0,5 – низкая.

Поскольку оценки экспертов считаются случайными величинами, то целесообразно проводить проверку значимости коэффициента W, путем определения вероятности согласованности их мнений с помощью распределения c²: c ² = N (m-1) W £ c ² _табл (a, k), (3.27) где a – уровень значимости, k = m -1 – число степеней свободы.

Пример. 3.12. Шесть экспертов (N = 6) ранжируют пять (m = 5) элементов (Х₁, Х₂, Х₅) по их важности. Результаты приведены в таблице. Определить суммарную ранжировку этих элементов и коэффициент конкордации. Проверить значимость коэффициента конкордации, если табличное значение c ² для 1% уровня значимости и 4-х степеней (n = m -1 = 5-1 = 4) свободы равно 13,28.

Решение

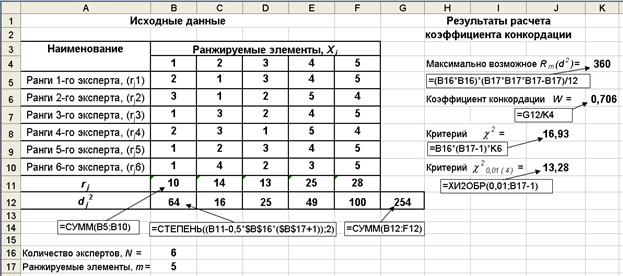
Рис. 3. 19. Исходные данные, расчетные формулы и результаты расчета коэффициента конкордации

1. По каждому j -му столбцу рассчитывается значение r_j , по формуле (3.23), см. ячейки (B11:F11) табл. на рис. 3.19.

2. По формуле (3.24) рассчитывается величина R(d ²), для этого предварительно вычисляются частные значения d _j² (см. ячеки (B12: F12)) и затем эти значения суммируются в ячейке G12, значение R(d ²) = 254.

3. Рассчитывается максимально возможное значение величины R_m(d ²) с использованием формулы (3.25), оно находится в ячейке K4 и составляет R_m(d ²) = 360.

4. Рассчитывается коэффициент конкордации W по формуле (3.26), он принимает значение равное 0,706, которое находится в ячейке K6. Чем ближе значение W к единице, тем сильнее согласованность между экспертами.

5. Проверяется значимость рассчитанного коэффициента W по критерию c ². С этой целью вначале вычисляется значение c ² для фактических значений, по формуле (3.27), оно находится в ячейке J8 и составляет 16,93.

Затем с помощью статистической функции Excel ХИ2ОБР для заданного в условии уровня значимости и k = 4 степеней свободы определяется табличное значение критерия c ²_кр = 13,28.

Далее проводится сравнение фактического значения c ² =16,93 с критическим c ²_кр = 13,28, и поскольку выполняется неравенство c ² > c ²_кр, то можно сделать вывод об удовлетворительной согласованности мнений экспертов в оценке ранжируемых элементов.