Методика составления уравнений колебаний экипажа

Для составления уравнений колебаний применяются методы аналитической механики в обобщенных координатах. Напомним, что положение механической системы может определяться набором n независимых параметров, в минимальном числе, однозначно определяющих положение всех точек рассматриваемой системы и называемых обобщенными координатами системы q_j (j=1,..., n). Число n называют числом степеней свободы механической системы.

Дифференциальные уравнения движения механической системы в обобщенных координатах (уравнения Лагранжа второго рода) имеют, как известно из курса теоретической механики, следующий вид:

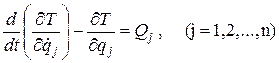(5.1)

При составлении уравнений Лагранжа необходимо, прежде всего, записать кинетическую энергию системы в функции обобщенных координат и скоростей

Кинетическая энергия системы твердых тел определяется как сумма кинетических энергий всех входящих в ее состав тел. Кинетическая энергия твердого тела определяется в зависимости от вида движения тела:

а) при поступательном движении твердого тела:

;

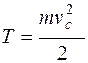v_c – скорость центра масс тела.

б) при вращении вокруг неподвижной оси

;

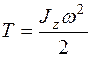J_z – момент инерции тела относительно оси вращения;

ω – угловая скорость вращения.

в) при плоскопараллельном движении

;

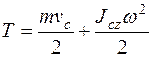J_cz – момент инерции тела относительно оси, проходящей через центр масс, перпендикулярно плоскости движения.

Рассмотрим механическую систему, состоящую из N материальных точек и имеющую n степеней свободы, на которую наложены голономные стационарные неосвобождающие связи. Предположив, что система имеет устойчивое положение равновесия, будем отсчитывать от этого положения обобщенные координаты 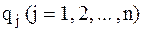. В соответствии с предположением о малости колебаний будем считать обобщенные координаты, их скорости и ускорения величинами первого порядка малости.

В силу стационарности связей скорость k-й точки системы

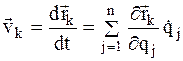, (3.2)

где 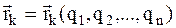– радиус – вектор этой точки.

Тогда кинетическая энергия системы будет равна

,

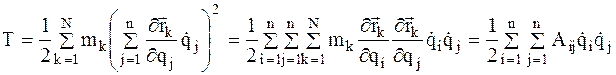где 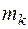– масса k-й точки, .

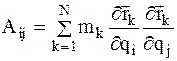Как и 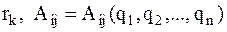, то есть являются в общем случае функциями обобщенных координат.

Разлагая 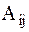в ряд Маклорена в окрестности положения равновесия

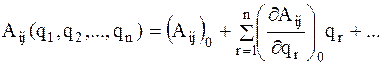
будем в силу малости колебаний учитывать только первый член разложения. Обозначим 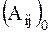через 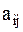и назовем обобщенными инерционными коэффициентами, причем в силу симметрии () 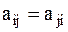. Окончательно получим

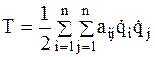. (3.3)

Кинетическая энергия представляет собой однородную квадратичную форму обобщенных скоростей 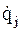с коэффициентами, являющимися функциями обобщенных координат q_j и не зависящими явно от времени:

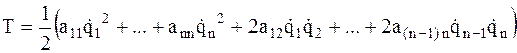. (3.4)

В аналитической механике каждой обобщенной координате 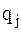соответствует обобщенная сила – 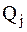, которая находится из выражения для элементарной работы (или мощности) действующих на механическую систему активных сил на ее возможном перемещении. Если вычислить сумму элементарных работ активных сил, действующих на точки системы на возможном перемещении системы, то соответствующая формула может быть представлена в виде:

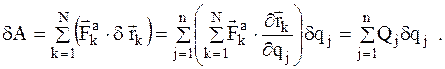
где 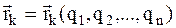- радиус-вектор 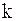- той точки 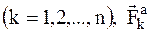- действующая на эту точку активная сила. Поэтому часто обобщенные силы определяют как коэффициенты, стоящие в выражении суммы элементарных работ активных сил при соответствующих обобщенных возможных перемещениях.

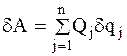(3.5)

В общем случае сила 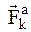, действующая на 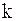-ю точку системы, может быть функцией положения точки 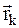, ее скорости 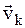и времени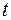

Тогда обобщенные силы Q_j могут быть представлены в виде

(3.6)

где 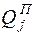–составляющая обобщенной силы от потенциальных сил;

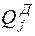– составляющая обобщенной силы от диссипативных сил;

– составляющая обобщенной силы от сил, зависящих от времени и действующих извне.

Составляющая обобщенной силы от потенциальных сил выражается через потенциальную энергию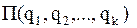

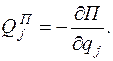(j=1,..,n) (3.7)

Потенциальная энергия механической системы, на которую действуют силы тяжести и силы упругости определяется следующим образом:

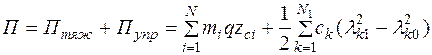
где N–число тел, входящих в систему, m_i–массы тел, q–ускорение свободного падения, z_ci–вертикальные перемещения центров масс тел, N₁–общее число упругих элементов в системе, c_j–жесткости упругих элементов, λ_k1, λ_k0 – конечная и начальная деформации упругих элементов. При вычислении потенциальной энергии величины z_ci, λ_k1 и λ_k0 должны быть выражены через обобщенные координаты q_j.

Составляющая обобщенной силы от диссипативных сил выражается через диссипативную функцию Рэлея 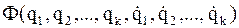, соответственно как

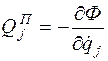(j=1,..,k) (3.8)

Диссипативная функция Рэлея учитывает наличие в системе элементов, обусловленных силами вязкого трения. Вязкое сопротивление пропорциональное скорости относительных перемещений тел системы, возникает в гидравлических гасителях колебаний (демпферах). Функция Рэлея определяется следующим образом:

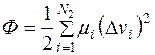
где N₂–число установленных демпферов, 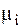–коэффициенты демпфирования, 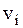–относительные скорости перемещений точек крепления демпферов к телам системы, выраженные через обобщенные скорости .

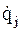Потенциальную энергию системы 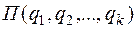разложим в ряд Маклорена в окрестности положения равновесия:

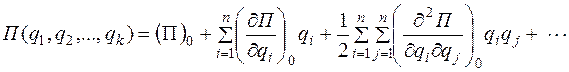
Первый член в разложении равен нулю, поскольку потенциальную энергию и обобщенные координаты отсчитывают от положения равновесия; вторые члены в разложении также равны нулю, так как в положении равновесия потенциальная энергия системы имеет экстремум и, следовательно, 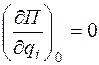; кроме того, в разложении отброшены члены, порядок которых выше второго (в силу предположения о малости колебаний).

Обозначим 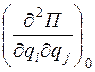через 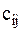и назовем квазиупругими коэффициентами, причем 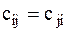. Окончательно имеем

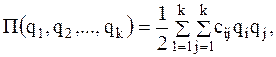(3.9)

то есть потенциальная энергия представляет собой квадратичную форму относительно обобщенных координат. Подставив выражение потенциальной энергии (3.9) в (3.7), получим составляющую обобщенной силы от потенциальных сил

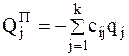. (3.10)

Учитывая выражение для скорости (3.2), запишем диссипативную функцию Рэлея для системы с n степенями свободы

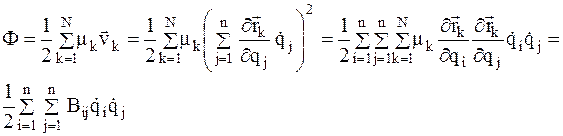
Здесь коэффициенты 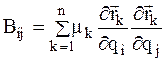в общем случае являются функциями обобщенных координат

.

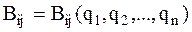Так как диссипативная функция Рэлея уже содержит величины второго порядка малости (произведения обобщенных скоростей), то в разложении 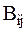в ряд Маклорена удержим только первые члены разложения – значения коэффициентов 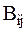в положении равновесия .

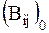Обозначим 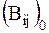через 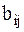и назовем их обобщенными диссипативными коэффициентами, причем 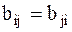. Тогда

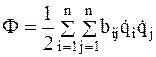(3.11)

Функция Ф представляет собой неотрицательную квадратичную форму. Если же Ф является положительно-определенной квадратичной формой, то диссипация называется полной.

Подставив выражение (3.11) в (3.8) получим составляющую обобщенной силы от диссипативных сил

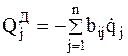. (3.12)

С учетом полученных выражений для 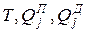уравнения Лагранжа второго рода для малых колебаний в линейной системе с 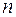степенями свободы примут вид

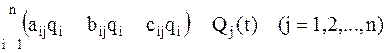. (3.13)