Влияние сопротивления на вынужденные колебания

Рис.87

Рис.86

Рис.85

Первое, что надо отметить, при p = k (частота возмущающей силы равна частоте свободных колебаний) амплитуда увеличивается до бесконечности.

Это явление называется резонансом.

Как известно из курса высшей математики, при p = k решение (17) не будет удовлетворять уравнению (15). Частное решение надо искать в другом виде:

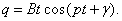
Подставив его в уравнение (15), получим:

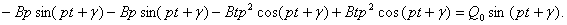
Отсюда 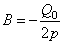и частное решение, определяющее вынужденные колебания при резонансе, получится таким

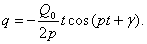(19)

Видим, что амплитуда колебаний беспредельно равномерно увеличивается (рис.86). Амплитуда не сразу становится бесконечно большой. И даже малая возмущающая сила может раскачать систему до больших амплитуд и вызвать разрушение конструкции.

Интересен еще один случай, при котором частота р возмущающей силы близка к частоте свободных колебаний, 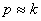, но не равна ей.

Воспользуемся решением (17), положив для простоты 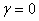. Пусть в начале движения координата и скорость равнялись нулю (при t = 0 q = 0 и 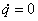). Подставим эти начальные условия в уравнения

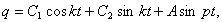
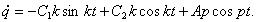
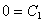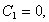
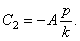Получим два уравнения: и из которых находим Тогда уравнение колебаний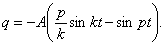

Так как 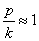и 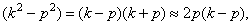то, по (16),

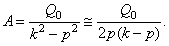
Кроме того 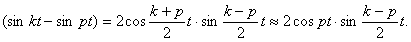Уравнение движения получится таким

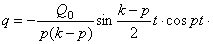(20)

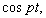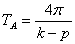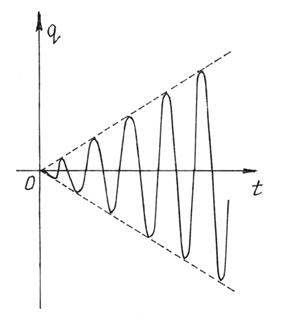
Рассматривая функцию, стоящую перед как амплитуду колебаний, замечаем, что она изменяется по гармоническому закону с периодом от нуля до максимального значения 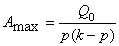(рис.87).

Сами колебания совершаются с частотой р и периодом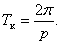

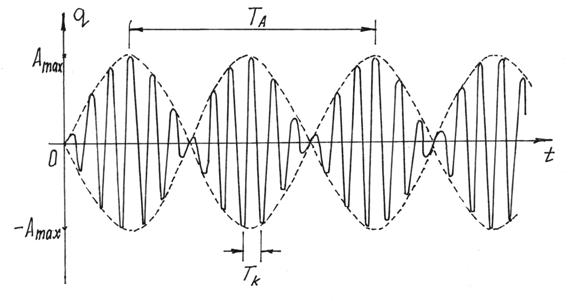
Чем ближе частота возмущающей силы р к частоте k, т.е. чем ближе к резонансу, тем больше будет период амплитуды 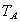и больше амплитуда . И тем больше будет похож график на рис.87 на график на рис.86, изображающий колебания при резонансе. Эти колебания с периодически изменяющейся амплитудой называются биениями. Такое явление часто встречается, например, в радиотехнике.

Мы исследовали вынужденные колебания под действием возмущающей силы, изменяющейся по гармоническому закону. Но нередко она оказывается более сложной. Приходится использовать специальные математические методы, чтобы получить более-менее точный результат.

Если возмущающая сила периодическая и ее можно разложить в ряд Фурье, то решение может оказаться не очень сложным.

Пусть возмущающая сила описывается периодической функцией Q = Q (t) с периодом 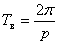, р – частота изменения этой функции. И пусть конструкция ее позволяет разложить функцию в ряд Фурье:

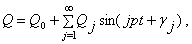
где 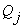и 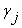- коэффициенты Фурье, определяемые по специальным формулам.

Частное решение дифференциального уравнения (15) получится в виде ряда:

.

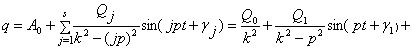
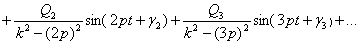Количество s членов этого ряда стараются иметь не очень большим, если ряд хорошо сходится.

Решение получается как сумма нескольких синусоид («гармоник») с кратными частотами. Наименьшая частота р – называется основной частотой.

Интересно, что в полученном решении возможно несколько резонансов, столько, сколько гармоник: при p = k, 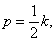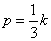и т.д.

Если учесть сопротивление среды пропорциональное скорости, как это было сделано выше, дифференциальное уравнение колебаний получится таким

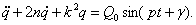(21)

Решение его состоит из общего и частного решений. Общее мы уже находили выше. Например, при малом сопротивлении (n < k)

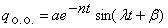, где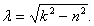

Частное решение будем искать в виде 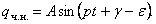Чтобы определить коэффициенты А и 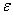, подставим это решение в уравнение (21). Получим

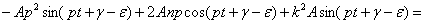
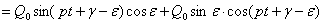
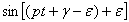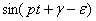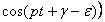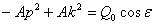(правую часть уравнения (21) представили как синус суммы двух углов: ). Полученное уравнение обратится в тождество, если будут выполнены два условия (сгруппировав члены, содержащие и :

и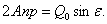

Из этих уравнений получим

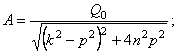
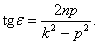(22)

Полное решение уравнения (21) будет таким

(23)

Очевидно, за счет сопротивления с течением времени первый член стремится к нулю. Поэтому можно заключить, что установившиеся вынужденные колебания и с учетом сопротивления среды будут гармоническими.

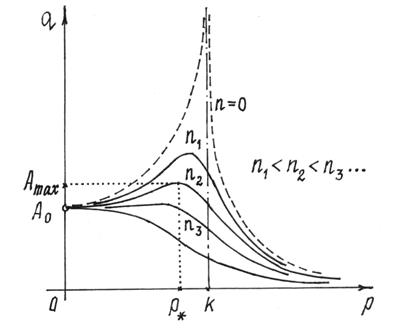
Причем, во-первых, частота колебаний равна частоте изменения возмущающей силы; во-вторых, колебания не зависят от начальных условий и, в-третьих, амплитуда колебаний А зависит от частоты р и от сопротивления среды, характеризующегося коэффициентом n.

График этой зависимости от р и n дан на рис.88.