Под струной понимают тонкую нить, которая может свободно изгибаться.
Пусть струна находится под действием сильного начального натяжения 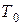 . Если вывести струну из положения равновесия и подвергнуть действию какой-нибудь силы, то струна начнет колебаться.
. Если вывести струну из положения равновесия и подвергнуть действию какой-нибудь силы, то струна начнет колебаться.
Рассмотрим малые, поперечные и плоские колебания струны, т.е. такие колебания, при которых отклонения точек струны от положения покоя малы, в любой момент времени все точки струны находятся в одной и той же плоскости, и каждая точка струны колеблется, оставаясь на одном и том же перпендикуляре к прямой, соответствующей состоянию покоя струны.
Принимая эту прямую за ось Ох, обозначим через u = и (х, t) отклонение точек струны от положения равновесия в момент времени t. При каждом фиксированном значении t график функции u = и (х, t) на плоскости хОи дает форму струны в момент времени t.
Функция u = и (х, t) удовлетворяет дифференциальному уравнению
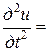
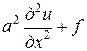 ,
,
где 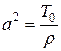 ,
, 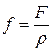 ,
, 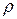 − масса единицы длины (линейная плотность струны), F − сила, действующая на струну перпендикулярно оси абсцисс и рассчитанная на единицу длины.
− масса единицы длины (линейная плотность струны), F − сила, действующая на струну перпендикулярно оси абсцисс и рассчитанная на единицу длины.
Если внешняя сила отсутствует, т.е. f = 0, то получится уравнение свободных колебаний струны
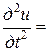
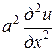 .
.
Решение уравнения колебаний струны методом характеристик
(методом Даламбера)
Для полного определения движения струны нужно задать в начальный момент времени форму и скорость струны, т.е. положение ее точек и их скорость в виде функций абсцисс х этих точек.
Пусть
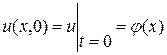 ,
, 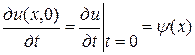 .
.
Эти условия называются начальными условиями задачи. Другими словами необходимо решить задачу Коши.
Приведя уравнение
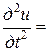
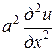
к каноническому виду, получим уравнение
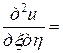 0,
0,
где 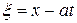 и
и 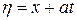 .
.
Общее решение последнего уравнения запишется в виде
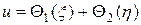 ,
,
где 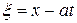 ,
, 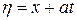 ,
, 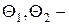 произвольные функции.
произвольные функции.
Таким образом
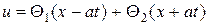 − решение Даламбера.
− решение Даламбера.
Используя начальные условия, найдем функции 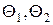 :
:
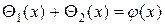 ,
,
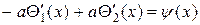 .
.
Интегрируя последнее уравнение на отрезке 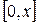 , получим
, получим
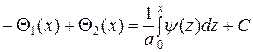 ,
,
где С − произвольная постоянная. Из уравнений
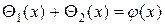 ,
,
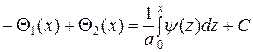
находим
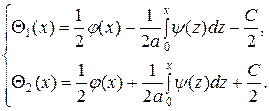
Теперь решение задачи Коши запишется
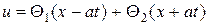 =
=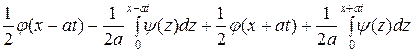
или
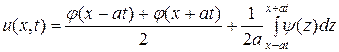 − формула Даламбера.
− формула Даламбера.
Пример. Найти решение уравнения
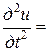
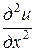 ,
,
если 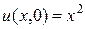 ,
, 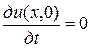 .
.
□ Здесь а = 1, 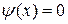 . Следовательно,
. Следовательно,
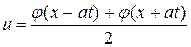 , где
, где 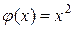 .
.
Таким образом,
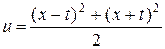 или
или 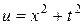 . ■
. ■
Пример. Найти форму струны, определяемой уравнением
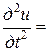
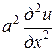
в момент времени 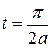 , если
, если 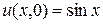 ,
, 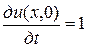 .
.
□ Имеем 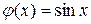 ,
, 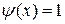 . Следовательно,
. Следовательно,
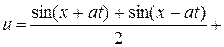
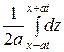 ,
,
т.е.
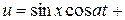
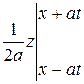 или
или 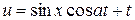 .
.
Если 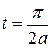 , то
, то 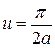 , т.е. струна параллельна оси абсцисс. ■
, т.е. струна параллельна оси абсцисс. ■
Решение уравнения колебаний струны, закрепленной на концах, методом разделения переменных (методом Фурье)
Метод разделения переменных (или метод Фурье) является типичным для решения многих задач математической физики.
Пусть требуется найти решение уравнения
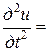
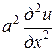 ,
,
удовлетворяющее начальным условиям
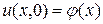 ,
, 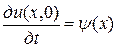
и граничным (краевым) условиям
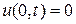 ,
, 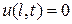 .
.
Граничные (краевые) условия показывают, что концы струны закреплены в точках х = 0 и х = l.
Будем искать (не равное тождественно нулю) частное решение уравнения в виде произведения двух функций, одна из которых зависит только от х, а другая − только от t,
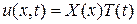 .
.
Подставляя это выражение в заданное уравнение, получим
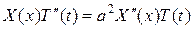 .
.
Разделяя переменные (Х = Х (х), T = T (t)), получим
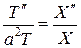 .
.
Это равенство двух отношений, левая часть которого зависит только х, а правая − только t, возможно только в том случае, когда эти части равны постоянному числу. Обозначим его через 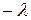 ,
, 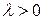 , т.е.
, т.е.
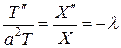 .
.
В результате получим два дифференциальных уравнения
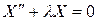 ,
, 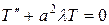 .
.
Общие решения этих уравнений:
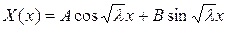 ,
, 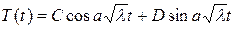 ,
,
где A, B, C, D − произвольные постоянные.
Тогда
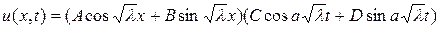 .
.
Постоянные А и В можно найти, используя краевые условия. Так как 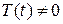 , то Х (0) = 0 и Х (l) = 0. Следовательно,
, то Х (0) = 0 и Х (l) = 0. Следовательно,
Х (0) = А = 0, 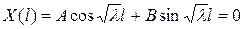 ,
,
т.е. А = 0 и 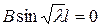 и в силу того, что
и в силу того, что 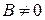 , имеем
, имеем 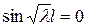 . Отсюда
. Отсюда
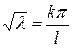 (k = 1, 2, …).
(k = 1, 2, …).
Итак, получено
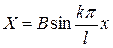 .
.
Найденные значения 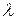 называются собственными значениями для данной краевой задачи, а соответствующие им функции
называются собственными значениями для данной краевой задачи, а соответствующие им функции 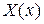 называются собственными функциями.
называются собственными функциями.
По найденным значениям 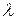 получаем
получаем
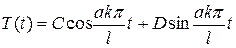
и
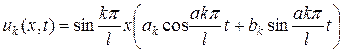 (k = 1, 2, …).
(k = 1, 2, …).
Индекс k в последнем выражении означает, что каждому значению k соответствуют свои значения постоянных С и D, которые записываем в виде 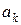 и
и 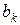 (постоянную В включаем
(постоянную В включаем 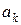 и
и 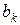 ) и свое решение
) и свое решение 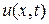 .
.
Так как заданное уравнение является линейным и однородным, то сумма решений также является решением, т.е.
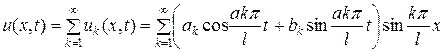 .
.
Этот ряд будет решением заданного уравнения, если коэффициенты 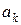 и
и 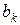 таковы, что сходится сам ряд, а также ряды, получающиеся после двукратного дифференцирования по х и по t. При этом решение должно удовлетворять начальным условиям.
таковы, что сходится сам ряд, а также ряды, получающиеся после двукратного дифференцирования по х и по t. При этом решение должно удовлетворять начальным условиям.
Из условия 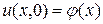 следует
следует
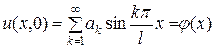 .
.
Если функция 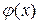 разлагается в ряд Фурье в промежутке (0, l) по синусам, то
разлагается в ряд Фурье в промежутке (0, l) по синусам, то
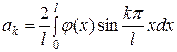 . (1)
. (1)
Из условия 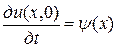 имеем
имеем
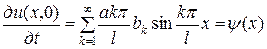 .
.
Определяем коэффициенты Фурье этого ряда:
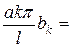
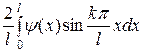
или
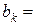
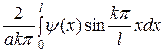 . (2)
. (2)
Таким образом, решение уравнения колебания струны может быть представлено как сумма бесконечного ряда
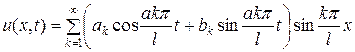 ,
,
где 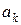 и
и 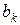 определяются по формулам (1) и (2).
определяются по формулам (1) и (2).
Замечание. Если положить 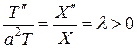 , то уравнения для определения
, то уравнения для определения  и
и  имели бы вид
имели бы вид  и
и 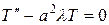 . Общее решение первого из них
. Общее решение первого из них 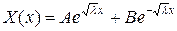 не удовлетворяет граничным условиям.
не удовлетворяет граничным условиям.
Пример. Струна, закрепленная на концах х = 0 и х = l, имеет в начальный момент форму параболы 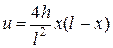 . Определить смещение точек струны от оси абсцисс, если начальные скорости отсутствуют.
. Определить смещение точек струны от оси абсцисс, если начальные скорости отсутствуют.
□ Имеем 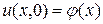
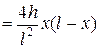 ,
, 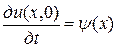 = 0,
= 0, 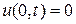 ,
, 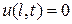 .
.
Решением является функция
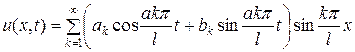 .
.
Находим коэффициенты ряда. Так как 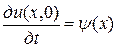 = 0, то
= 0, то 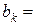 0. Определим коэффициент
0. Определим коэффициент 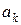 :
:
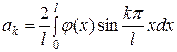 =
= 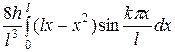 =
= 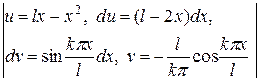 =
=
=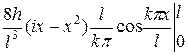 +
+ 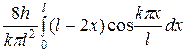 =
=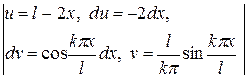 =
=
= 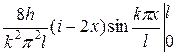 +
+ 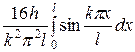 =
= 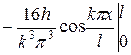 =
= 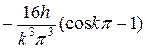 =
=
= 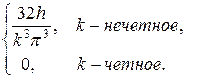
Подставляя найденные значения 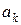 и
и 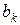 в выражение ряда, получим
в выражение ряда, получим
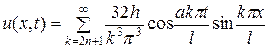 , п = 0, 1, 2,… ■
, п = 0, 1, 2,… ■
 2014-02-09
2014-02-09 14639
14639
