Особенности задачи Лагранжа по отношению к общей задаче оптимального управления, записанной выше: отсутствие неинтегральной части критерия, зачастую граничные условия фиксированы.
Пример: для теплообменника, описываемого ДУ 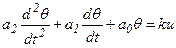 , найти оптимальное управление, обеспечивающее изменение температуры на выходе от
, найти оптимальное управление, обеспечивающее изменение температуры на выходе от 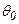 до
до 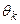 при
при 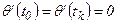 за заданное время и с минимальным расходом энергии, т.е.
за заданное время и с минимальным расходом энергии, т.е. 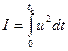 .
.
Для общей постановки задачи поиск экстремалей проводят по уравнениям Эйлера (Эйлера-Лагранжа):
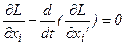 ,
, 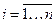 ;
;
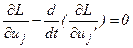 ,
,  .
.
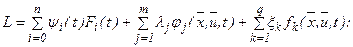
 L - функция Лагранжа;
L - функция Лагранжа;
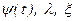 - коэффициенты Лагранжа.
- коэффициенты Лагранжа.
Если функционал не содержит производных, т.е. 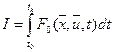 , а уравнение ограничений можно записать в форме Коши:
, а уравнение ограничений можно записать в форме Коши:
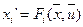 ;
;
либо это можно обеспечить введением новых переменных, тогда систему уравнений для поиска управляющих воздействий можно записать проще.
Подставляя дифференциальные уравнения 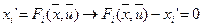 в функцию
в функцию
Лагранжа
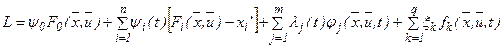 ,
,
где 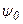 - коэффициент, задаваемый произвольно, (обычно его принимают равным +1 или -1),
- коэффициент, задаваемый произвольно, (обычно его принимают равным +1 или -1),
перенесем слагаемые с производными в левую часть
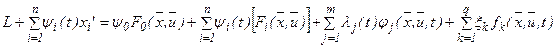 .
.
Функцию 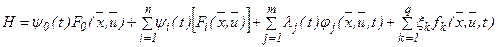
или 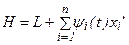 , не содержащую производных, называют функцией Гамильтона.
, не содержащую производных, называют функцией Гамильтона.
Запишем уравнения Эйлера для функции Гамильтона. Для этого в систему уравнений Эйлера -Лагранжа
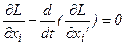 ,
, 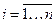 ;
;
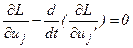 ,
,  ;
;
подставим 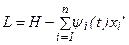 и, учитывая, что Н не содержит производных от x и u, получим
и, учитывая, что Н не содержит производных от x и u, получим
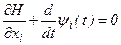 ,
, 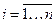 ;
;
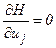 ,
,  ;
;
или
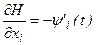 ,
, 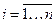 ;
;
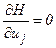 ,
,  .
.
Получаем более простую систему ДУ для нахождения 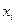 и
и 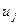 .
.
 2015-06-05
2015-06-05 674
674








