2015-06-05
364
1.
· Производная от неопределенного интеграла равна подынтегральной функции:
,
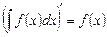· дифференциал от неопределенного интеграла равен подынтегральному выражению:
.
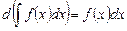► Пусть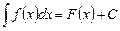 
.
Тогда
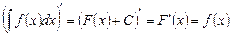
и дифференциал
. ◄
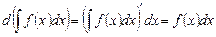2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
.
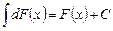► Действительно, так как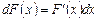 
, то
. ◄
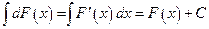Замечание. Свойства 1 и 2 показывают, что в случае, когда знаки дифференцирования и интегрирования стоят друг за другом, то они уничтожаются.
3. Постоянный множитель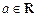 
, 
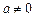, можно выносить за знак неопределенного интеграла:
.
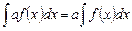► Действительно, пусть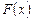 
– первообразная функции 
: 
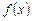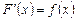. Тогда 
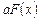– первообразная функции 
:
.
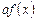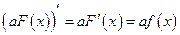Отсюда следует, что
,
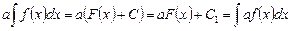где постоянная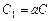 
. ◄
4. Неопределенный интеграл от суммы двух функций равен сумме интегралов от этих функций:
.
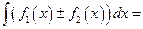
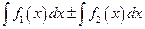► Пусть 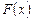и 
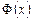– первообразные функци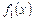й 
и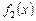 
: 
, 
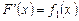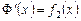. Тогда функции 
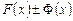являются первообразными функций 
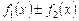. Следовательно,
. ◄
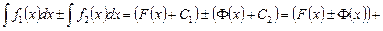
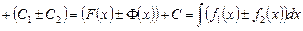5. Если 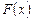– первообразная функции 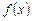, то
.
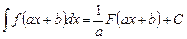► Действительно,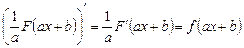 
. ◄
|
|
|
4. Таблица основных неопределенных интегралов. Так как интегрирование есть действие, обратное дифференцированию, то большинство из приводимых формул может быть получено обращением соответствующих формул дифференцирования.
Таблица основных неопределенных интегралов
1. 
;
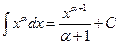
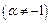2. 
;
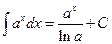
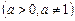3. 
;
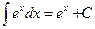4. 
;
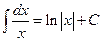5. 
;
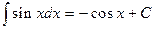6. 
;
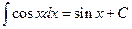7. 
;
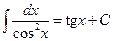8. 
;
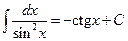9. 
;
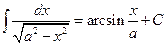10. 
;
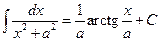11. 
;
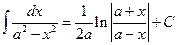12. 
;
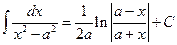13. 
;
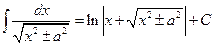14. 
;
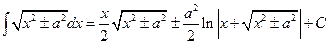15. 
.
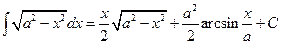Интегралы в приводимой выше таблице называются табличными. Их следует знать наизусть.
В справедливости приведенных выше формул можно убедиться, продифференцировав их правые части.
Если первообразная 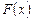функция 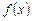является элементарной функцией, то говорят, что интеграл 
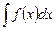выражается в элементарных функциях или функция 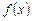интегрируема в конечном виде. Однако не всякий интеграл от элементарной функции выражается в элементарных функциях. Используя основные правила интегрирования, можно находить интегралы от более сложных функций.
В отличие от дифференциального исчисления, где, пользуясь таблицей производных, можно найти производную или дифференциал любой заданной функции, в интегральном исчислении нет общих приемов вычисления неопределенных интегралов, а разработаны лишь частные методы, позволяющие свести данный (искомый) интеграл к табличному.
