ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
Лекция 1. ПЕРВООБРАЗНАЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1. Определение первообразной функции.
2. Неопределенный интеграл и его свойства.
3. Основные свойства неопределенного интеграла
4. Таблица основных неопределенных интегралов.
5. Основные методы интегрирования.
1. Определение первообразной функции. Основной задачей дифференциального исчисления является нахождение производной 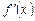 или дифференциала
или дифференциала 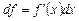 функции
функции 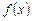 . В интегральном исчислении решается обратная задача: по заданной функции
. В интегральном исчислении решается обратная задача: по заданной функции 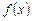 требуется найти такую функцию
требуется найти такую функцию 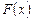 , что
, что 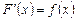 .
.
Таким образом, основной задачей интегрального исчисления является восстановление функции 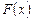 по известной производной этой функции.
по известной производной этой функции.
Определение 1. Функция 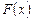 , называется первообразной функции
, называется первообразной функции 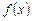 на интервале
на интервале 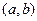 , если для любого
, если для любого 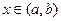 выполняется равенство
выполняется равенство 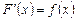 .
.
Замечание 1. Если 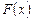 является первообразной функции
является первообразной функции 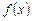 на интервале
на интервале 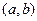 , то
, то 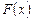 непрерывна на
непрерывна на 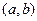 . (Почему?)
. (Почему?)
Замечание 2. В определении первообразной 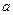 и
и 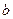 могут быть как конечными, так и бесконечными.
могут быть как конечными, так и бесконечными.
Пример. Первообразной функции 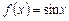 на множестве
на множестве 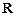 является функция
является функция 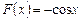 , так как
, так как 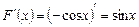
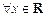 .
.
Очевидно, что первообразными будут также и любые функции 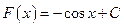 , где
, где 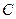 – постоянная, поскольку
– постоянная, поскольку 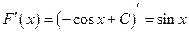 .
.
В дифференциальном исчислении было доказано, что если 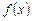 дифференцируема, то ее производная
дифференцируема, то ее производная 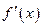 единственна. Приведенный выше пример показывает, что первообразная таким свойством не обладает.
единственна. Приведенный выше пример показывает, что первообразная таким свойством не обладает.
Теорема 1. Если функция 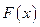 является первообразной функции
является первообразной функции 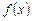 на
на 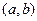 , то множество всех первообразных для функции
, то множество всех первообразных для функции 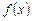 совпадает с множеством функций вида
совпадает с множеством функций вида 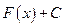 , где
, где 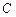 – постоянная.
– постоянная.
► Пусть 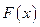 – первообразная функции
– первообразная функции 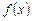 на
на 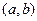 . Тогда для функции
. Тогда для функции 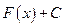 имеем
имеем 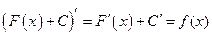
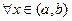 , т.е.
, т.е. 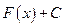 является первообразной функции
является первообразной функции 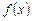 .
.
Пусть теперь 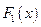 – некоторая другая, отличная от
– некоторая другая, отличная от 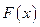 , первообразная функции
, первообразная функции 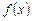 , т.е.
, т.е. 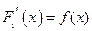 . Тогда для функции
. Тогда для функции 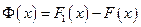
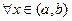 имеем
имеем
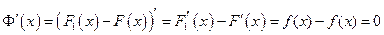 ,
,
т.е. 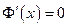
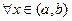 .
.
Возьмем две произвольные точки 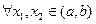 . На отрезке
. На отрезке 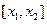 для функции
для функции 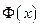 выполнены все условия теоремы Лагранжа и поэтому справедлива формула
выполнены все условия теоремы Лагранжа и поэтому справедлива формула
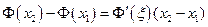 , где
, где 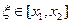 .
.
А поскольку 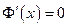
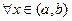 , то отсюда следует, что
, то отсюда следует, что 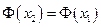 , а это означает, что
, а это означает, что 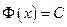 . Таким образом,
. Таким образом, 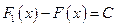 , или
, или 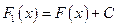 .◄
.◄
Вопрос: всякая ли функция имеет первообразную?
Справедлива следующая теорема.
Теорема 1. Любая непрерывная на интервале 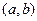 функция
функция 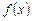 имеет на этом интервале первообразную
имеет на этом интервале первообразную 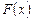 .
.
 2015-06-05
2015-06-05 415
415







