Пример решения 6.1

Согласно своему варианту записываем уравнение химической реакции, например:

K₂Cr₂O₇ + Ti₂(SO₄)₃ + H₂SO₄ = Cr₂(SO₄)₃ + Ti(SO₄)₂ + H₂O + K₂SO₄.

Уравнивание стехиометрических коэффициентов ионно-электронным методом проводим по определенному алгоритму.

1) Проставим для всех элементов степени окисления:

+ + = + + + .

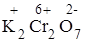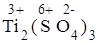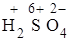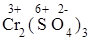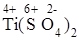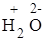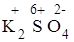2) Выясним элементы, меняющие степень окисления в результате реакции и определим, какое вещество выполняет роль окислителя (принимает электроны), а какое – роль восстановителя (отдает электроны).

В данной реакции изменяют степени окисления элементы Cr и Ti, при этом K₂Cr₂O₇ выполняет роль окислителя, а Ti₂(SO₄)₃ – роль восстановителя, H₂SO₄ играет роль среды.

3) Запишем реакцию в ионно-электронном виде и подчеркнем окислитель и восстановитель. Для этого учитываем диссоциацию молекул на ионы, а слабые электролиты (например, Н₂О, оксиды и сульфиды металлов), если они встречаются в реакции, оставляем в молекулярном виде. Получаем:

2K⁺ + (Cr₂O₇) ^2- + 2Ti ³⁺ + 3(SO₄)^2- + 2H⁺ + (SO₄)^2– =

= 2Cr ³⁺ + 3(SO₄)^2- + Ti ⁴⁺ + 2(SO₄)^2- + H₂O + 2K⁺ + (SO₄)^2-.

4) Записываем полуреакции окисления и восстановления, рассматривая только подчеркнутые частицы. Сравниваем количество основных элементов справа и слева и, при необходимости, вводим уравнивающие коэффициенты (в данном случае ставим 2 перед Ti⁴⁺).

(Cr₂O₇)^2- → 2Cr³⁺;

окислитель

2Ti³⁺ → 2Ti⁴⁺.

восстановитель

5) Отметим число принятых электронов в полуреакции восстановления и число отданных электронов в полуреакции окисления.

(Cr₂O₇)^2- + 6 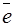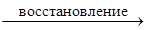2Cr³⁺;

2Ti³⁺ – 2 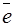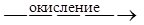2Ti⁴⁺.

6) Проводим в каждой строчке ионное уравнивание. Баланс по кислороду проводим в виде H₂O, а по водороду – в виде Н⁺.

В данном случае в верхней полуреакции справа вводим 7H₂O, а в левую часть – добавляем 14 Н⁺. Во второй полуреакции изменений нет. Получаем следующее:

14Н⁺ +(Cr₂O₇)^2- + 6 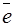→ 2Cr³⁺ + 7H₂O;

2Ti³⁺ – 2 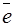→ 2Ti⁴⁺.

7) Проводим электронный баланс, принимая во внимание, что число отданных восстановителем электронов всегда равно числу электронов, принятых окислителем. Справа ставим вертикальную черту, находим наименьшее общее кратное и проставляем соответствующие коэффициенты.

14Н⁺ +(Cr₂O₇)^2- + 6 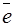→ 2Cr³⁺ + 7H₂O; 1

2Ti³⁺ – 2 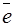→ 2Ti⁴⁺. 3

8) Складываем левые и правые части полуреакций, умножив на соответствующие коэффициенты:

14H⁺ + (Cr₂O₇)^2- + 6Ti³⁺ = 2Cr³⁺ + 7H₂O + 6Ti⁴⁺.

9) Теперь под знаком равенства поставим короткую вертикальную черту и для элементов, стоящих слева, добавим связанные с ними частицы, которые раньше мы не учитывали. Как видно из 3): для (Cr₂O₇)^2- это 2К⁺, для 2Ti³⁺ – это 3(SO₄)^2-, а для 2Н⁺ – это (SO₄)^2-. Те же самые частицы записываем справа от черты. Получаем следующее:

14H⁺ + (Cr₂O₇)^2- + 6Ti³⁺ = 2Cr³⁺ + 7H₂O + 6Ti⁴⁺;

7(SO₄)^2- + 2K⁺ + 9(SO₄)^2- | 7(SO₄)^2- + 2K⁺ + 9(SO₄)^2-.

10) Учитывая добавленные ионы, составляем полное уравнение со всеми стехиометрическими коэффициентами:

K₂Cr₂O₇ +3Ti₂(SO₄)₃ +7H₂SO₄ = Cr₂(SO₄)₃ +6Ti(SO₄)₂ + 7H₂O+K₂SO₄.

Теперь определим термодинамическую вероятность протекания данной окислительно-восстановительной реакции. Как показано в теме III, для этого необходимо провести расчет убыли свободной энергии (Δ G ⁰₂₉₈ химической реакции).

Записываем из 7) полуреакции окисления и восстановления и, пользуясь данными Приложения 3, приводим для них справа значения электродных потенциалов (φ⁰):

14Н⁺+(Cr₂O₇)^2- 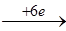2Cr³⁺+7H₂O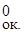; φ = φ 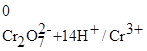= +1,33 В;

2Ti³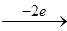⁺ 2Ti⁴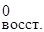⁺ φ = φ 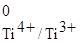= –0,04 В.

Рассчитываем ЭДС протекающего процесса (ε⁰):

ε⁰ 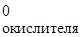= φ – φ 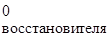= 1,33 - (-0,04) = 1,37 В.

Далее рассчитываем Δ G 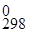химической реакции:

Δ G ⁰₂₉₈ = – zF ε⁰,

где z – число электронов, переданных от восстановителя к окислителю. С учетом электронного баланса z = 6;

F – число Фарадея, равное 96500 Кл/моль.

Чтобы ответ получить в кДж, вводим множитель 10^-3:

Δ G ⁰₂₉₈ = -6×96500×1,37×10^-3 = -793,2 кДж.

Так как Δ G ⁰₂₉₈ < 0, то данная реакция термодинамически вероятна, т.е. может протекать в прямом направлении.

Задание 6.2. Для двух металлов (табл. VI.2), находящихся в растворах своих солей с определенной концентрацией:

6.2.1. С оставьте схему гальванического элемента.

6.2.2. Запишите реакции, протекающие на катоде и аноде.

6.2.3. Рассчитайте ЭДС (ε⁰) гальванического элемента и Δ G ⁰₂₉₈ протекающей реакции.