Если функция распределения 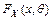 генеральной совокупности
генеральной совокупности 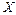 известна с точностью до параметра
известна с точностью до параметра 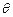 , то его интервальной оценкой или доверительным интервалом называется случайный интервал
, то его интервальной оценкой или доверительным интервалом называется случайный интервал 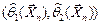 , который накрывает неизвестное значение параметра
, который накрывает неизвестное значение параметра 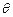 с заданной вероятностью
с заданной вероятностью 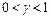 , т.е.
, т.е. 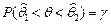 . Число
. Число 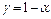 называется доверительной вероятностью, а число
называется доверительной вероятностью, а число 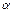 - уровнем значимости. Обычно используются значения
- уровнем значимости. Обычно используются значения 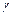 , равные
, равные 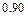 ,
, 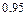 ,
, 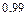 .
.
Точность интервальной оценки характеризуется длиной 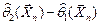 доверительного интервала и зависит от объёма
доверительного интервала и зависит от объёма 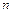 выборки и доверительной вероятности
выборки и доверительной вероятности 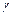 . Очевидно, что, чем меньше длина доверительного интервала, тем точнее оценка. Доверительный интервал, симметричный относительно точечной оценки
. Очевидно, что, чем меньше длина доверительного интервала, тем точнее оценка. Доверительный интервал, симметричный относительно точечной оценки 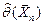 , определяется формулой
, определяется формулой 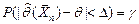 и имеет вид
и имеет вид 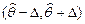 , где
, где 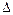 характеризует отклонение выборочного значения параметра от его истинного значения и называется предельной ошибкой выборки. Доверительные интервалы часто строятся в предположении, что выборка получена из генеральной совокупности, имеющей нормальное распределение.
характеризует отклонение выборочного значения параметра от его истинного значения и называется предельной ошибкой выборки. Доверительные интервалы часто строятся в предположении, что выборка получена из генеральной совокупности, имеющей нормальное распределение.
Доверительные интервалы для параметров 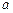 и
и 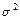 нормально распределённой генеральной совокупности.
нормально распределённой генеральной совокупности.
| Параметр | Точечная оценка | Доверительный интервал |
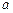 ( (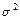 неизвестна) неизвестна) | 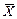 | 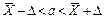 , где , где 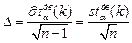 , , 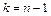 |
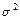 ( (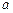 неизвестно) неизвестно) | 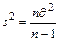 | 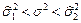 , где , где 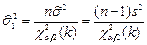 , , 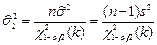 , , 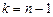 . . |
Доверительный интервал для параметра 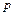 биномиального распределения.
биномиального распределения.
| Параметр | Точечная оценка | Доверительный интервал |
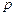 ( (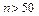 , , 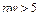 , , 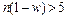 ) ) | 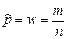 | 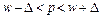 , где , где 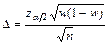 |
Здесь: 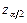 - корень уравнения
- корень уравнения 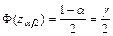 (приложение 6.2);
(приложение 6.2); 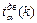 -критическая точка распределения Стьюдента (приложение 6.4);
-критическая точка распределения Стьюдента (приложение 6.4); 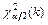 ,
, 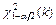 - критические точки распределения
- критические точки распределения 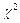 (приложение 6.3);
(приложение 6.3); 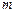 - число элементов в выборке, обладающих данным свойством.
- число элементов в выборке, обладающих данным свойством.
Необходимый объём выборки обеспечивающий заданное значение 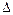 при оценивании параметров
при оценивании параметров 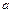 и
и 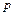 определяется, соответственно, соотношениями:
определяется, соответственно, соотношениями: 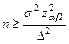 и
и 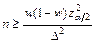 (
(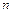 - целое число).
- целое число).
13.38 Предполагая, что распределение генеральных совокупностей является нормальным, найти 90%-ные доверительные интервалы для математического ожидания (среднего) и дисперсии следующих характеристик: а) ёмкость конденсатора, если 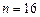 ,
, 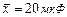 ,
, 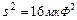 ; б) время безотказной работы электролампы, если
; б) время безотказной работы электролампы, если 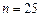 ,
, 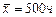 ,
, 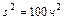 ; в) диаметр вала, если
; в) диаметр вала, если 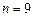 ,
, 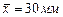 ,
, 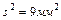 ; г) содержание углерода в ед. продукта, если
; г) содержание углерода в ед. продукта, если 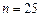 ,
, 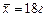 ,
, 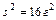 .
.
13.40 Получены следующие данные о годовом товарообороте (в млн. руб.) 100 продовольственных магазинов города:
 | [100,120) | [120,140) | [140,160) | [160,180) | [180,200] |
 |
Найти 95%-ный доверительный интервал для среднего товарооборота продовольственного магазина в городе.
13.41 Измерения твёрдости 16 образцов легированной стали (в условных единицах) дали следующие результаты:
13.1, 12.8, 11.9, 12.4, 13.5, 13.7, 12.0, 13.8, 10.6, 12.4, 13.5, 11.7, 13.9, 11.5, 12.5, 11.9.
В предположении, что выборка измерений получена из нормально распределённой генеральной совокупности, найти 95%-ные доверительные интервалы для математического ожидания и дисперсии генеральной совокупности.
13.42 Результаты 10 измерений ёмкости конденсатора дали следующие отклонения от номинального значения (пкФ):
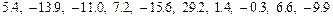 .
.
Найти 90%-ный доверительный интервал для дисперсии и среднего квадратичного отклонения, предполагая, что генеральная совокупность имеет нормальное распределение.
13.43 Из большой партии транзисторов одного типа были случайным образом отобраны и проверены 100 штук. У 36 транзисторов коэффициент усиления оказался меньше 10. Найти 95%-ный доверительный интервал для доли таких транзисторов во всей партии.
13.44 При осмотре 60 ящиков обнаружено 10 повреждённых. Найти 90%-ный доверительный интервал для доли повреждённых ящиков во всей партии.
13.45 Для оценки уровня безработицы в городе были отобраны случайным образом 100 человек рабочих специальностей. Из них 6 человек оказались безработными. Найти 90%-ный доверительный интервал для доли безработных рабочих в городе.
13.46 При проверке 100 деталей из большой партии обнаружено 10 бракованных деталей. Найти 95%-ный доверительный интервал для доли бракованных деталей во всей партии.
13.47 С автоматической линии, производящей подшипники, было отобрано 400 штук, причём 10 оказались бракованными. Найти 90%-ный доверительный интервал для вероятности появления бракованного подшипника. Сколько подшипников надо проверить, чтобы с вероятностью 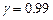 можно было утверждать, что вероятность
можно было утверждать, что вероятность 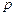 появления бракованного подшипника отличается от относительной частоты
появления бракованного подшипника отличается от относительной частоты 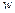 его появления не более чем на 5%?
его появления не более чем на 5%?
13.48 В 10000 сеансах игры с автоматом выигрыш появился 4000 раз. Найти 95%-ный доверительный интервал для вероятности выигрыша. Сколько сеансов игры следует провести, чтобы с вероятностью 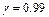 можно было утверждать, что вероятность
можно было утверждать, что вероятность 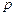 выигрыша отличается от его относительной частоты
выигрыша отличается от его относительной частоты 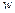 не более чем на 1%?
не более чем на 1%?
13.49 По результатам социологического исследования при опросе 1500 респондентов рейтинг президента (т.е. процент опрошенных, одобряющих его деятельность) составил 70%. Найти границы, в которых с доверительной вероятностью 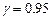 заключён рейтинг президента (при опросе всех жителей страны). Сколько респондентов надо опросить, чтобы с вероятностью
заключён рейтинг президента (при опросе всех жителей страны). Сколько респондентов надо опросить, чтобы с вероятностью 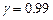 гарантировать предельную ошибку, допускаемую при определении рейтинга в результате социологического исследования, не превышающую 1%?
гарантировать предельную ошибку, допускаемую при определении рейтинга в результате социологического исследования, не превышающую 1%?
13.50 Высота самолёта определяется с помощью высотомера, средняя квадратичная ошибка которого 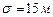 . Считая, что ошибки измерения высоты самолёта распределены по нормальному закону, определить, сколько надо иметь таких приборов на самолёте, чтобы с вероятностью
. Считая, что ошибки измерения высоты самолёта распределены по нормальному закону, определить, сколько надо иметь таких приборов на самолёте, чтобы с вероятностью 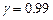 предельная ошибка измерения средней высоты самолёта была не более
предельная ошибка измерения средней высоты самолёта была не более 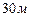 .
.
ОТВЕТЫ: 13.29 а) 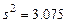 ; б)
; б) 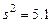 . 13.30
. 13.30 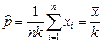 . 13.31
. 13.31 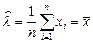 13.32
13.32 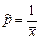 13.33
13.33 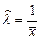 13.34
13.34 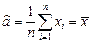 .,
., 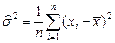 . 13.36
. 13.36 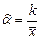 13.37
13.37 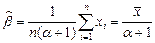
13.38 а) 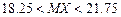 ,
, 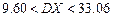 ; б)
; б) 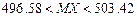 ,
, 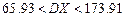 ;
;
в) 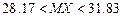 ,
, 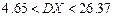 ; г)
; г) 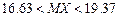 ,
, 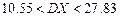 .
.
13.40 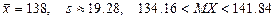 . 13.41
. 13.41 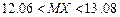 ,
, 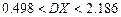 . 13.42
. 13.42 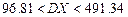 ;
; 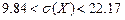 . 13.43
. 13.43 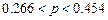 13.44
13.44 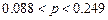 13.45
13.45 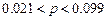 13.46
13.46 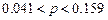 13.47
13.47 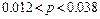 ;
; 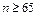 . 13.48
. 13.48 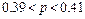 ;
; 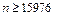 . 13.49
. 13.49 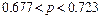 ;
; 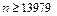 . 13.50 На самолёте должно быть не менее двух высотомеров.
. 13.50 На самолёте должно быть не менее двух высотомеров.
 2015-06-10
2015-06-10 4301
4301