Функция 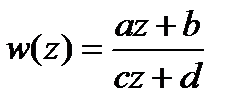 , где
, где 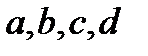 – комплексные числа, удовлетворяющие условию
– комплексные числа, удовлетворяющие условию 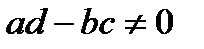 , называется дробно-линейной, а отображение, осуществляемое ею – дробно-линейным отображением. При
, называется дробно-линейной, а отображение, осуществляемое ею – дробно-линейным отображением. При 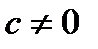 надо считать, что
надо считать, что 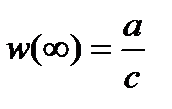 ,
, 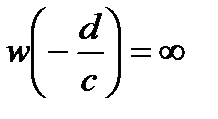 , а при
, а при 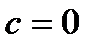 считать
считать 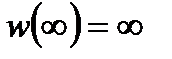 .
.
Существует единственная дробно-линейная функция, отображающая заданные три различные точки 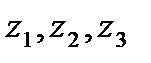 расширенной комплексной плоскости в заданные три различные точки
расширенной комплексной плоскости в заданные три различные точки 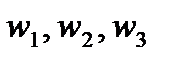 соответственно. Она находится из соотношения
соответственно. Она находится из соотношения
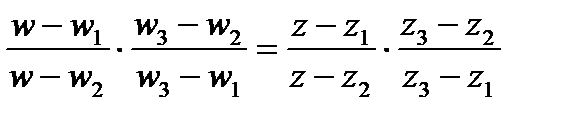 , (1)
, (1)
которое надо рассматривать как уравнение относительно 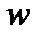 . При этом, если некоторые из чисел
. При этом, если некоторые из чисел 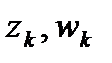 равны
равны 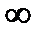 , то дробь, у которой в числителе и знаменателе присутствует
, то дробь, у которой в числителе и знаменателе присутствует 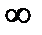 , надо считать равной 1. Например, если w1 =
, надо считать равной 1. Например, если w1 = 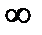 , то надо считать
, то надо считать
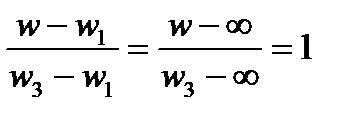 .
.
Точки 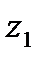 и
и 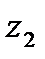 называются симметричными относительно окружности
называются симметричными относительно окружности 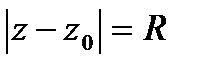 , если они расположены на одном луче, выходящем из центра
, если они расположены на одном луче, выходящем из центра 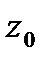 , и
, и
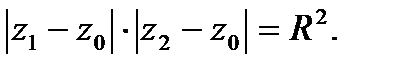
Дробно-линейная функция отображает окружность в окружность (круговое свойство), а точки, симметричные относительно окружности – в точки, симметричные относительно образа этой окружности (свойство симметрии). При этом прямую надо рассматривать как окружность, проходящую через ∞ и замкнутую в бесконечно удаленной точке.
|
|
|
Чтобы найти образ ориентированной окружности (или прямой) при дробно-линейном отображении 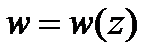 , надо взять на данной окружности три различные точки
, надо взять на данной окружности три различные точки 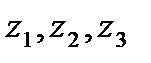 согласно направлению обхода, найти их образы
согласно направлению обхода, найти их образы 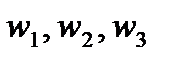 и провести через них окружность, которая и будет образом данной окружности. Направление обхода на ней надо брать от точки
и провести через них окружность, которая и будет образом данной окружности. Направление обхода на ней надо брать от точки 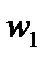 к точке
к точке 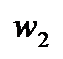 и от
и от 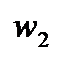 к
к 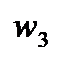 .
.
Чтобы найти образ части окружности или прямой (дуги, отрезка, луча) при дробно-линейном отображении 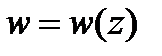 , надо взять на ней три точки: начальную
, надо взять на ней три точки: начальную 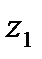 , какую-нибудь «среднюю»
, какую-нибудь «среднюю» 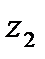 и конечную
и конечную 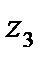 , найти их образы
, найти их образы 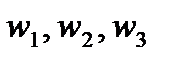 , провести через них окружность и взять ту часть, для которой
, провести через них окружность и взять ту часть, для которой 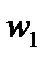 – начальная точка,
– начальная точка, 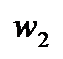 – «средняя точка» и
– «средняя точка» и 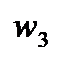 – конечная точка.
– конечная точка.
Чтобы найти образ области, ограниченной дугами окружностей и частями прямых, надо выбрать на границе области направление обхода так, чтобы область оставалась слева, и найти образы всех частей границы с учетом их направлений. Эти образы в совокупности образуют некоторую ориентированную замкнутую линию, может быть, неограниченную, т.е. замкнутую в 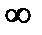 . Тогда область, остающаяся слева от этой линии, будет образом исходной области.
. Тогда область, остающаяся слева от этой линии, будет образом исходной области.
Чтобы найти какое-нибудь одно конформное отображение области 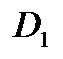 , ограниченной окружностью (или прямой), на подобную же область
, ограниченной окружностью (или прямой), на подобную же область 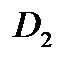 , надо выбрать направления обходов границ
, надо выбрать направления обходов границ 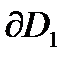 и
и 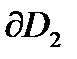 областей
областей 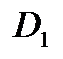 и
и 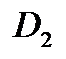 так, чтобы области оставались слева. Затем на границах
так, чтобы области оставались слева. Затем на границах 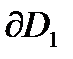 и
и 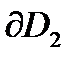 взять согласно направлениям обходов по три различных точки
взять согласно направлениям обходов по три различных точки 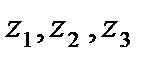 и
и 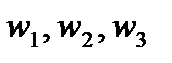 соответственно и из уравнения (1) найти дробно-линейную функцию
соответственно и из уравнения (1) найти дробно-линейную функцию 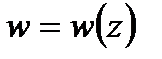 , которая и будет одним из конформных отображений области
, которая и будет одним из конформных отображений области 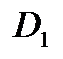 на область
на область 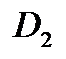 .
.
|
|
|
В общем случае конформное отображение единичного круга 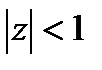 на единичный круг
на единичный круг 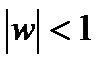 имеет вид:
имеет вид:
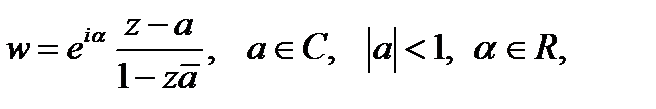
конформное отображение верхней полуплоскости Im z > 0 на единичный круг 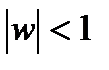 имеет вид:
имеет вид:
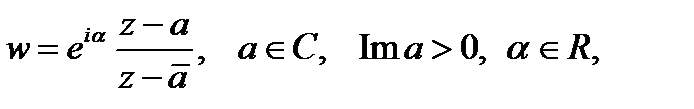
конформное отображение верхней полуплоскости Im z > 0 на верхнюю полуплоскость Im w > 0 имеет вид:
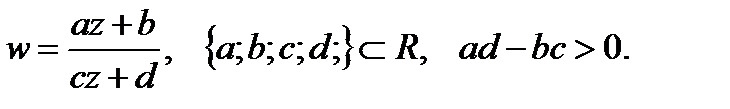
Задачи
1. Найти дробно-линейную функцию, отображающую точки 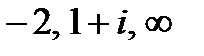 соответственно в точки
соответственно в точки 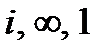 .
.
Решение:Подставив в соотношение (1) заданные значения
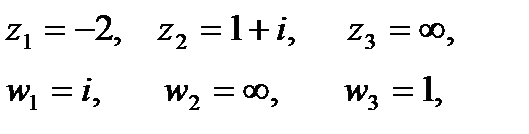
получим:
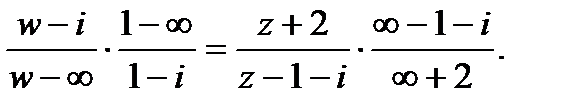
Считая
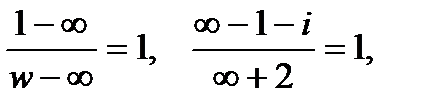
получим:
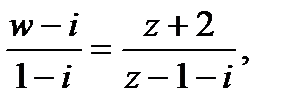
откуда находим:
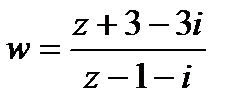 .
.
2. Найти точку, симметричную с точкой 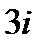 относительно окружности
относительно окружности 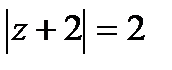 .
.
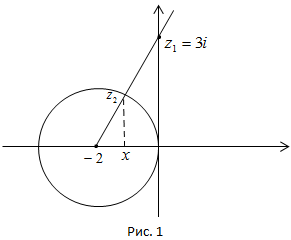
Решение. Из рис. 1, на котором изображены точка z1 = 3  и окружность
и окружность 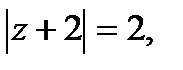 видно, что искомая симметричная точка расположена внутри окружности и имеет вид
видно, что искомая симметричная точка расположена внутри окружности и имеет вид 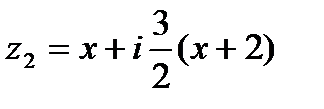 , где x > -2. Это следует из подобия соответствующих треугольников. Подставив z1, z2 в равенство
, где x > -2. Это следует из подобия соответствующих треугольников. Подставив z1, z2 в равенство
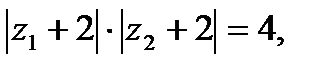
получим: 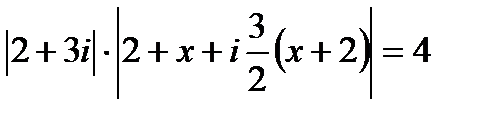 , откуда с учетом неравенства x > -2 находим
, откуда с учетом неравенства x > -2 находим 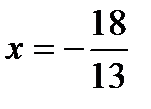 . Тогда
. Тогда 
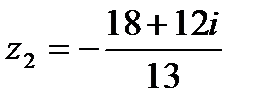 .
.
3. Найти образы окружностей 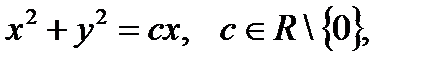 при отображении
при отображении 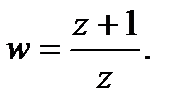
Решение. Так как
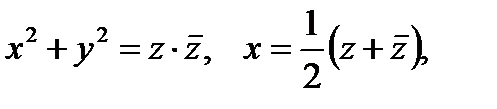
то уравнения окружностей имеют вид:
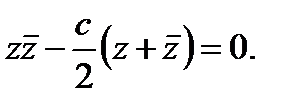
Подставив сюда 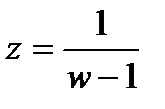 , найденное из уравнения
, найденное из уравнения 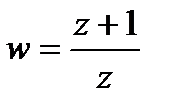 , получим:
, получим:
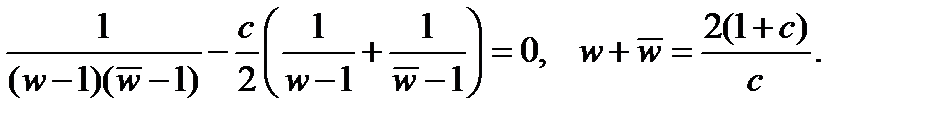
Считая 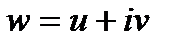 , получим семейство вертикальных прямых
, получим семейство вертикальных прямых
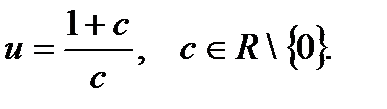
4. Найти образы области D при отображении 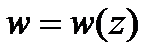 , если
, если
а) 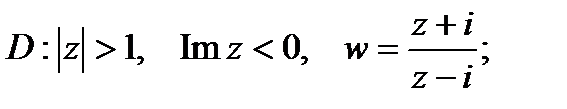
б) 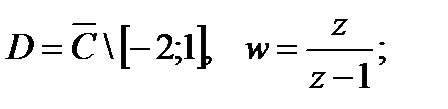
в) 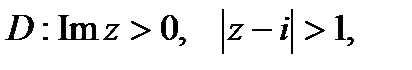
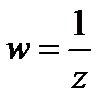 .
.
Решение. а) Область D и положительная ориентация ее границы указаны на рис. 2.
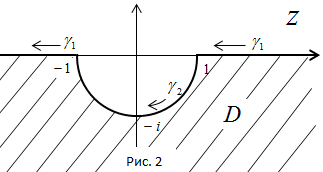
Граница 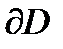 области в данном случае состоит из двух частей: полуокружности
области в данном случае состоит из двух частей: полуокружности 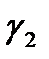 и двух лучей, которые надо рассматривать как одну непрерывную часть
и двух лучей, которые надо рассматривать как одну непрерывную часть 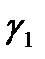 прямой Im z = 0, так как прямая считается окружностью, проходящей через
прямой Im z = 0, так как прямая считается окружностью, проходящей через 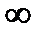 , т.е. непрерывной кривой, замкнутой в
, т.е. непрерывной кривой, замкнутой в 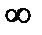 . На этих лучах, как на одной части границы
. На этих лучах, как на одной части границы 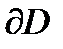 , выберем начальную точку z1 = -1, среднюю точку z2 =
, выберем начальную точку z1 = -1, среднюю точку z2 = 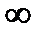 , конечную точку z3 = 1 и найдем их образы
, конечную точку z3 = 1 и найдем их образы
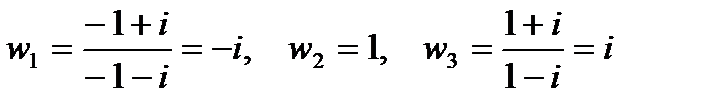 .
.
Проведем через точку –  , 1,
, 1,  окружность и возьмем ту часть, для которой -
окружность и возьмем ту часть, для которой -  – начало, 1 – средняя точка,
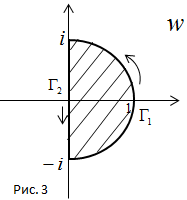
– начало, 1 – средняя точка,  – конец. Ею будет дуга Г1 (рис. 3). Направление обхода на дуге Г1 берется от –
– конец. Ею будет дуга Г1 (рис. 3). Направление обхода на дуге Г1 берется от –  к 1 и от 1 к
к 1 и от 1 к  . Эта дуга будет образом совокупности двух лучей
. Эта дуга будет образом совокупности двух лучей 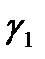 .
.
Найдем образ полуокружности 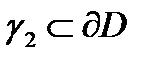 . Образами начала 1, средней точки –
. Образами начала 1, средней точки –  и конца -1 полуокружности
и конца -1 полуокружности 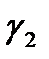 будут точки
будут точки  , 0 и –
, 0 и –  соответственно. Окружность, проходящая через эти точки, есть прямая Re w = 0, поэтому образом полуокружности
соответственно. Окружность, проходящая через эти точки, есть прямая Re w = 0, поэтому образом полуокружности 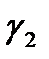 будет отрезок Г2 с концами
будет отрезок Г2 с концами  и –
и –  , направленный сверху вниз (рис. 3).
, направленный сверху вниз (рис. 3).
Следовательно, образом границы 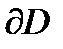 при отображении
при отображении 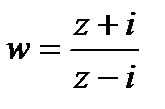 будет замкнутая кривая Г1
будет замкнутая кривая Г1  Г2, направленная против часовой стрелки, а образом области D – полукруг, изображенный на рис. 3.
Г2, направленная против часовой стрелки, а образом области D – полукруг, изображенный на рис. 3.
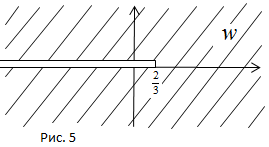
б) В данном случае область D представляет собой расширенную комплексную плоскость С с разрезом по отрезку [-2; 1] (рис. 4).
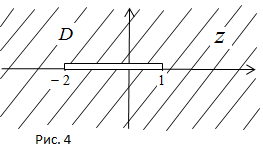
Так как дробно-линейная функция отображает 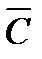 на
на 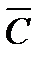 , то образом области D будет
, то образом области D будет 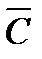 , из которой надо выкинуть образ отрезка [-2;1]. Так как образами начала -2, «средней точки» 0 и конца 1 при отображении
, из которой надо выкинуть образ отрезка [-2;1]. Так как образами начала -2, «средней точки» 0 и конца 1 при отображении 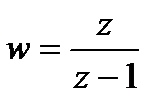 будут соответственно точки
будут соответственно точки 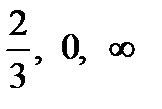 , то образом отрезка [-2;1] будет луч
, то образом отрезка [-2;1] будет луч  . Тогда образом области D будет плоскость с разрезом по лучу
. Тогда образом области D будет плоскость с разрезом по лучу 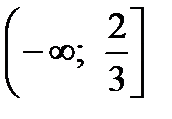 (рис.5).
(рис.5).
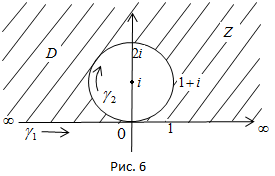
в) Граница области D состоит из прямой 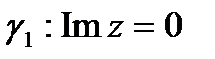 , ориентированной слева направо, и окружности
, ориентированной слева направо, и окружности 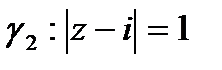 , ориентированной против часовой стрелки (рис. 6). При отображении
, ориентированной против часовой стрелки (рис. 6). При отображении 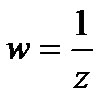 точки
точки 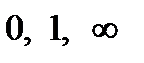 , расположенные на прямой
, расположенные на прямой 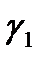 согласно направлению обхода, переходят соответственно в точки
согласно направлению обхода, переходят соответственно в точки 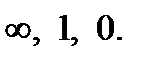 Значит, прямая
Значит, прямая 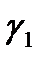
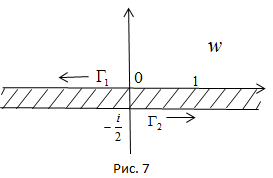
переходит в прямую 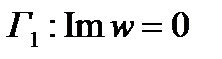 , ориентированную справа налево (рис.7). Аналогично, взяв на окружности
, ориентированную справа налево (рис.7). Аналогично, взяв на окружности 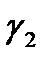 точки 2
точки 2  , 1+
, 1+  , 0 и вычислив их образы
, 0 и вычислив их образы 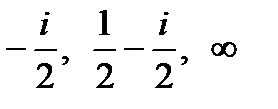 , найдем образ окружности
, найдем образ окружности 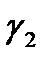 . Им будет прямая
. Им будет прямая 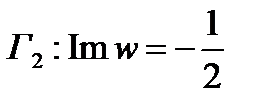 , ориентированная слева направо. Значит, образом границы
, ориентированная слева направо. Значит, образом границы 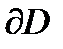 будет совокупность прямых Г1 и Г2, а образом области D будет полоса
будет совокупность прямых Г1 и Г2, а образом области D будет полоса 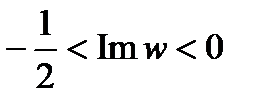 , изображенная на рис. 7.
, изображенная на рис. 7.
5. Найти какое-нибудь конформное отображение области 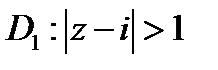 на полуплоскость
на полуплоскость 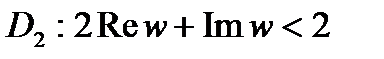 .
.
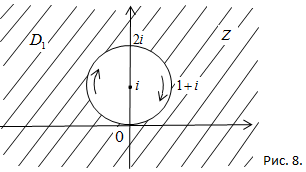
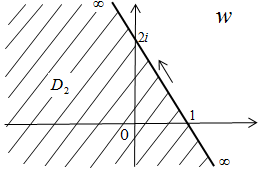
Решение. Выберем направления обходов границ областей D1 и D2 (рис.8) так, чтобы области оставались слева. Согласно этим направлениям на границах 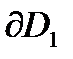 и
и 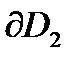 возьмем по три точки
возьмем по три точки 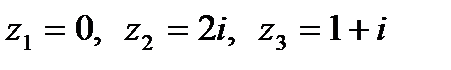 и
и 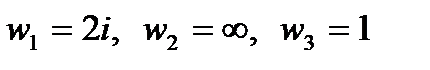 и, подставив их в уравнение (1), найдем дробно-линейное отображение
и, подставив их в уравнение (1), найдем дробно-линейное отображение

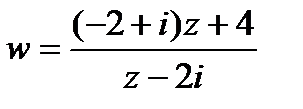 ,
,
которое и будет одним из искомых конформных отображений.
6. Найти конформное отображение 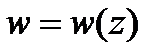 верхней полуплоскости
верхней полуплоскости 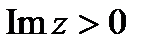 на единичный круг
на единичный круг 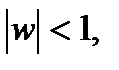 удовлетворяющее условиям
удовлетворяющее условиям 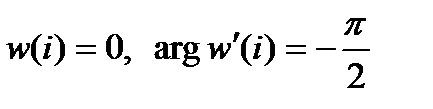 .
.
|
|
|
Решение. Так как общий вид конформного отображения верхней полуплоскости на единичный круг имеет вид
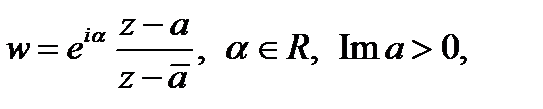
то числа 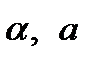 надо выбрать так, чтобы
надо выбрать так, чтобы
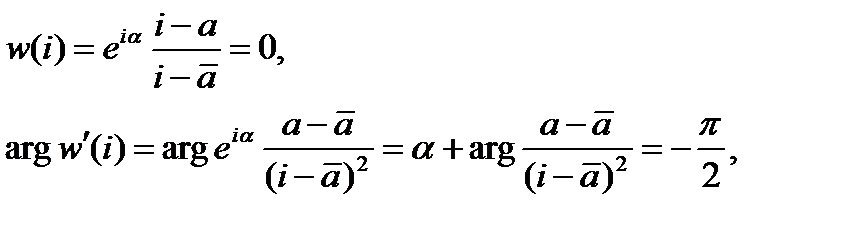
откуда 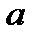 =
= 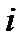 ,
,
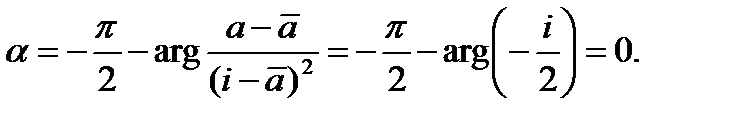
Значит, искомое конформное отображение имеет вид 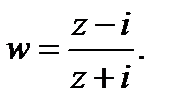
7. Найти конформное отображение 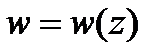 полуплоскости Re z + Im z < 0 на круг
полуплоскости Re z + Im z < 0 на круг 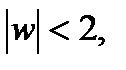 удовлетворяющее условиям
удовлетворяющее условиям 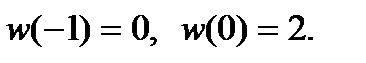
Решение. Так как любое конформное отображение области, ограниченной окружностью (или прямой), на подобную область является дробно-линейным, то согласно свойству симметрии дробно-линейной функции при искомом отображении точка 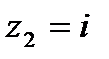 , симметричная точке
, симметричная точке 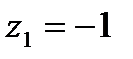 относительно прямой Re z + Im z = 0 (рис. 9), перейдет в точ-
относительно прямой Re z + Im z = 0 (рис. 9), перейдет в точ-
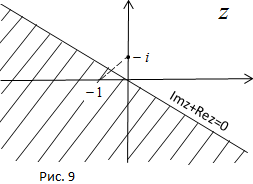

ку 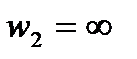 , симметричную точке
, симметричную точке 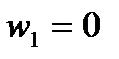 относительно окружности
относительно окружности 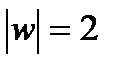 (рис. 10), которая является образом прямой Re z + Im z = 0, при искомом отображении. Следовательно, точки
(рис. 10), которая является образом прямой Re z + Im z = 0, при искомом отображении. Следовательно, точки 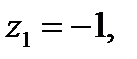
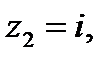
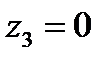 переходят соответственно в точки
переходят соответственно в точки 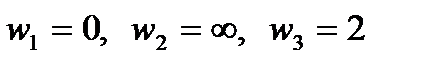 , подставив которые в уравнение (1), найдем искомое отображение:
, подставив которые в уравнение (1), найдем искомое отображение:
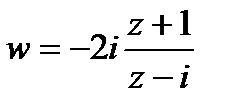 .
.
8. Найти конформное 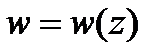 отображение круга
отображение круга 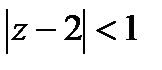 на круг
на круг 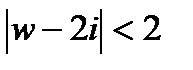 , удовлетворяющее условиям
, удовлетворяющее условиям 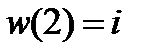 ,
, 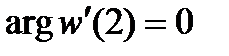 .
.
Решение. Точке 2 симметрична относительно окружности 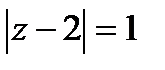 точка
точка 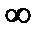 , а точке
, а точке 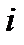 симметрична относительно окружности
симметрична относительно окружности 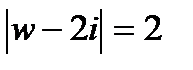 точка -2
точка -2 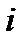 . Следовательно, при искомом дробно-линейном отображении точки 2 и
. Следовательно, при искомом дробно-линейном отображении точки 2 и 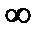 перейдут соответственно в точки
перейдут соответственно в точки 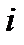 и 2
и 2 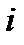 . Пусть в точку
. Пусть в точку 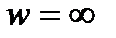 переходит некоторая неизвестная пока точка
переходит некоторая неизвестная пока точка 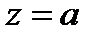 . Тогда дробно-линейное отображение, переводящее точки 2,
. Тогда дробно-линейное отображение, переводящее точки 2, 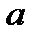 ,
, 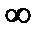 соответственно в точки
соответственно в точки 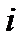 ,
, 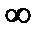 , -2
, -2 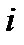 найдется из уравнения
найдется из уравнения
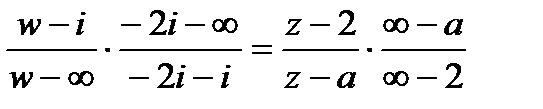 ,
,
откуда
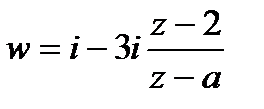 .
.
Для нахождения 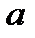 воспользуемся условием
воспользуемся условием 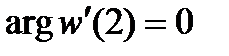 и условием
и условием 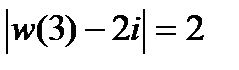 , означающим, что при искомом отображении граничная точка z = 3 круга
, означающим, что при искомом отображении граничная точка z = 3 круга 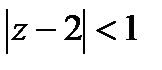 переходит в некоторую граничную точку круга
переходит в некоторую граничную точку круга 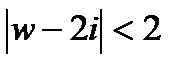 .
.
Из первого условия
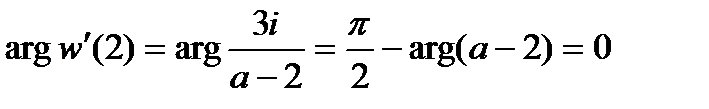
находим 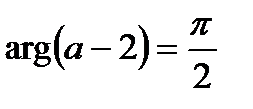 . Следовательно, комплексное число
. Следовательно, комплексное число 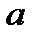 –2 имеет вид
–2 имеет вид
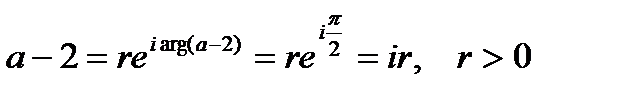 ,
,
откуда 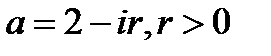 . Из второго условия
. Из второго условия
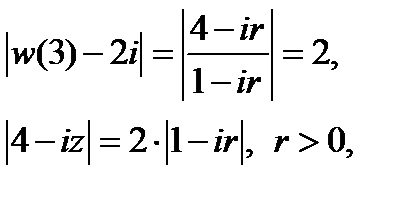
находим r = 2. Значит, 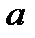 = 2 + 2
= 2 + 2 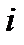 и
и
 2015-06-26
2015-06-26 26432
26432







