Окружностью называется линия, каждая точка 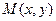 на которой находится на одинаковом расстоянии
на которой находится на одинаковом расстоянии 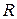 от заданной точки
от заданной точки 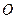 , называемой центром окружности. Величина
, называемой центром окружности. Величина 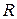 называется радиусом окружности.
называется радиусом окружности.
В прямоугольной системе координат уравнение окружности имеет вид
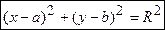 ,
,
где 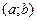 — координаты её центра,
— координаты её центра, 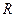 — радиус окружности.
— радиус окружности.
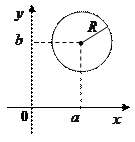
В частности, если центр окружности совпадает с началом координат, т.е. 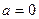 ,
, 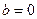 , то уравнение окружности примет вид:
, то уравнение окружности примет вид:
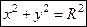
§ Признак уравнения окружности: коэффициент 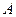 при
при 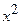 равен коэффициенту
равен коэффициенту 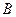 при
при 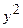 .
.
§ Свойства окружности:
Окружность имеет бесконечное множество осей симметрий.
Точки на окружности равноудалены от центра.
Пример. Найдите координаты центра и радиус окружности 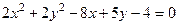 .
.
Разделив уравнение на 2, и сгруппировав члены уравнения, получим 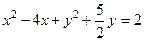 .
.
Дополним выражения 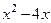 и
и 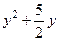 до полных квадратов, прибавив к первому двучлену 4, а ко второму
до полных квадратов, прибавив к первому двучлену 4, а ко второму 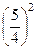 (одновременно к правой части прибавляется сумма этих чисел):
(одновременно к правой части прибавляется сумма этих чисел):
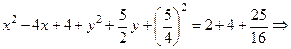
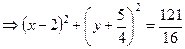 .
.
По формуле 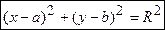 имеем
имеем 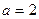 ,
, 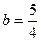 , т.е.
, т.е. 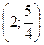 — координаты центра окружности;
— координаты центра окружности; 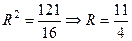 — радиус окружности.
— радиус окружности.
3. Эллипс
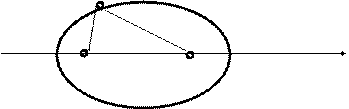
Эллипсом называется линия, для каждой точки 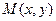 на которой сумма расстояний до двух заданных точек
на которой сумма расстояний до двух заданных точек 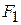 и
и 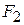 (фокусов эллипса) есть величина постоянная:
(фокусов эллипса) есть величина постоянная: 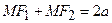 .
.
§ Уравнение эллипса с центром в начале координат:
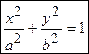 .
.
Числа 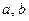 называются большой и малой полуосью эллипса.
называются большой и малой полуосью эллипса.
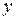

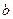
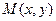
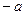
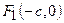
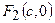

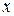
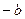
Между 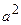 и
и 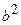 существует связь:
существует связь: 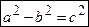 .
.
Точки 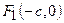 и
и 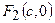 являются фокусами эллипса, причем
являются фокусами эллипса, причем 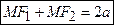 .
.
Свойство эллипса:эллипс имеет две оси симметрии 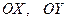 .
.
Признак уравнения эллипса: коэффициент 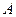 при
при 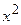 и коэффициент
и коэффициент 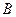 при
при 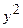 имеют одинаковый знак и по абсолютной величине не равны между собой.
имеют одинаковый знак и по абсолютной величине не равны между собой.
§ Уравнение эллипса со смещенным центром в точке 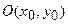 :
:
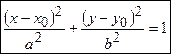
Пример. Дано уравнение эллипса 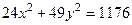 . Найдите длины его полуосей, координаты фокусов.
. Найдите длины его полуосей, координаты фокусов.
Запишем уравнение эллипса в каноническом виде, разделив обе его части на 1176:
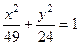 .
.
Отсюда 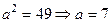 ,
, 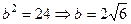 .
.
Используя соотношение (4), находим 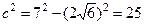 и
и 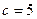 . Следовательно,
. Следовательно, 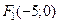 и
и 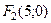 .
.
 2015-06-28
2015-06-28 8705
8705
