Свойства (аксиомы) операций в линейном пространстве.
Пусть f, g, h 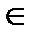 L,
L, 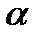 , b
, b 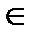 R.
R.
1. f + g = g + f (коммутативность),
2.. (f + g) + h = f +(g + h) (ассоциативность),
3. 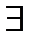 элемент 0
элемент 0 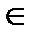 L: f + 0 = f (0 - нейтральный элемент)
L: f + 0 = f (0 - нейтральный элемент)
/ можно доказать, что нейтральный может быть только один /,
4. для  f
f 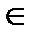 L,
L, 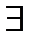 - f: f + (-f) = 0 (-f - противоположный элемент)
- f: f + (-f) = 0 (-f - противоположный элемент)
/ можно доказать, что для каждого элемента может быть только один противоположный /,
5. 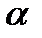 . (f + g) =
. (f + g) = 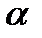 . f +
. f + 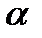 . g,
. g,
6. ( 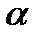 + b) . f =
+ b) . f = 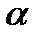 . f + b . f,
. f + b . f,
7. ( 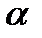 . b) . f =
. b) . f = 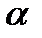 . ( b . f),
. ( b . f),
8. 1. f = f
/ из этого можно вывести, что -f = (- 1 ) . f /.
 2015-06-26
2015-06-26 412
412








