Предложение

Если A: R² → R², то A = ,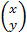

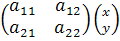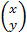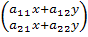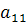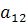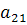т.е. A = , где , , и 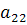- некоторые числа, определяемые спецификой отображения.

Доказательство.

Пусть задана некоторая точка 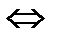некоторый вектор 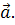В прямоугольной системе координат он имеет вид: 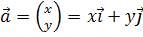, где 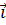, 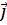– единичные векторы на осях координат.

Картинка!!!

Получаем, что .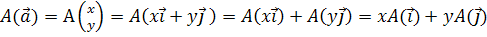

Видим, что образ вектора 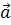определяется его координатам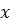и и 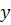, а также образами единичных векторов.

Пусть вектор 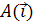имеет в той же системе координат координаты 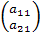, а вектор 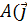) 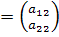. Тогда можно записать:

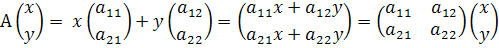
Что и требовалось доказать.

Замечание. Столбцами матрицы линейного преобразования являются координаты образов единичных базисных векторов.