Задать аналитически следующие отображения на R2.
1. Симметрия относительно оси Ox.
В примере 3 показано, что это отображение является линейным отображением. Обозначим его А. По доказанному предложению отображение в координатах имеет вид:
A 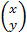 =
= 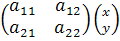 . Найдём коэффициенты матрицы.
. Найдём коэффициенты матрицы.
1 способ.
Образом вектора 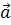 =
= 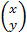 при симметрии относительно оси Ох является вектор A(
при симметрии относительно оси Ох является вектор A(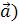 =
= 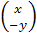 ,
,
т.е. 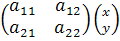 =
= 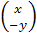 картинка!!!
картинка!!!
Покоординатно получаем:
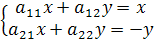 при всех x, y.
при всех x, y.
В первом уравнении правая часть не зависит от y => 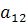 =0 =>
=0 => 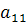 =1.
=1.
Во втором уравнении правая часть не зависит от x => 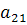 =0 =>
=0 => 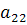 =-1.
=-1.
Значит, матрица отображения имеет вид: A = 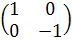 .
.
2 способ
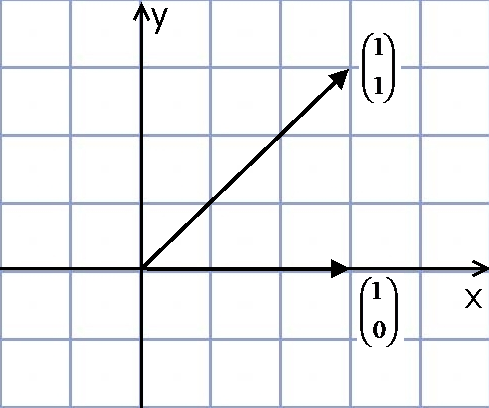 Для отыскания 4-х неизвестных коэффициентов матрицы составим 4 уравнения. Достаточно рассмотреть отображение двух конкретных векторов. Например, найдём образы векторов
Для отыскания 4-х неизвестных коэффициентов матрицы составим 4 уравнения. Достаточно рассмотреть отображение двух конкретных векторов. Например, найдём образы векторов 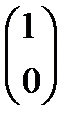 и
и 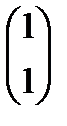 . Получаем
. Получаем
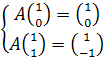 , т.е.
, т.е.
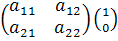 =
= 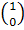 ;
; 
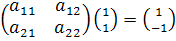
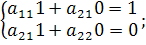
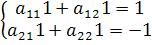
отсюда 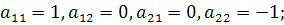
3 способ
Воспользуемся замечанием к утверждению теоремы. Найдём образы единичных векторов на осях координат:
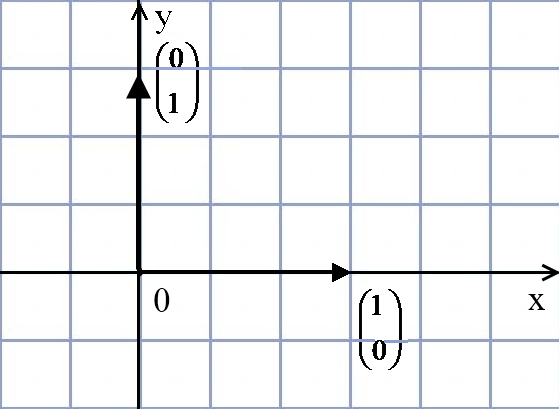
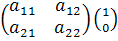 =
= 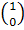 и
и 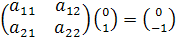 .
.
Координаты полученных векторов являются столбцами матрицы отображения: A = 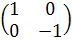 .
.
2. A – симметрия относительно Oy.
Отображение принципиально не отличается от предыдущего.
Используя 1 способ рассуждения, получаем: 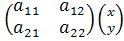 =
= 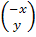 , т.е.
, т.е.
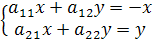 при всех x, y.
при всех x, y.
В первом уравнении правая часть не зависит от y => 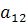 =0 =>
=0 => 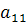 = -1.
= -1.
Во втором уравнении правая часть не зависит от x => 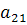 =0 =>
=0 => 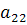 = 1.
= 1.
Значит, матрица отображения имеет вид: A = 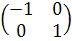 .
.
По 3 способу рассуждения достаточно найти образы единичных векторов:
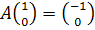 и
и 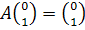 - эти векторы образуют столбцы матрицы.
- эти векторы образуют столбцы матрицы.
A= 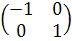 .
.
3. A – симметрия относительно прямой y=x.
Это отображение является линейным, как и две предыдущие осевые симметрии.
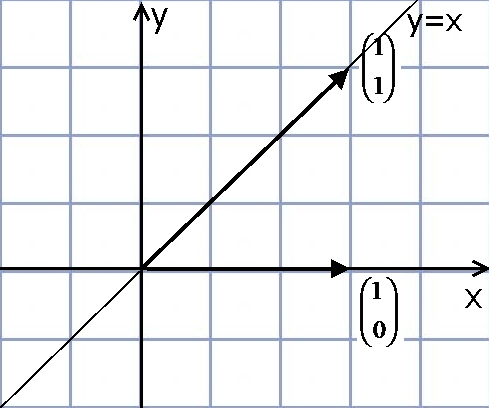
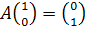 и
и 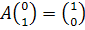
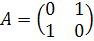
4. A – симметрия относительно y= -x.
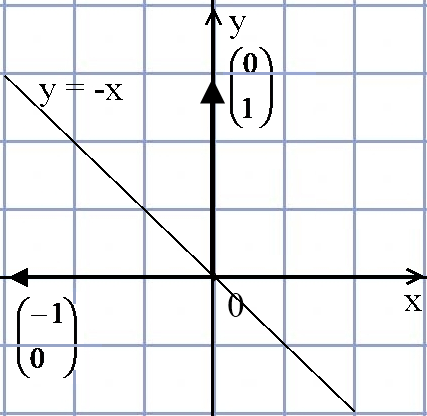
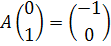
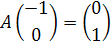 A =
A = 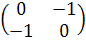 .
.
5. A – центральная симметрия (поворот на 180о).

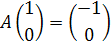
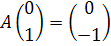
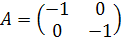
6. Поворот на угол α против часовой стрелки.
Рассмотрим единичные векторы 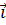 и
и 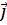 и найдём их образы.
и найдём их образы.
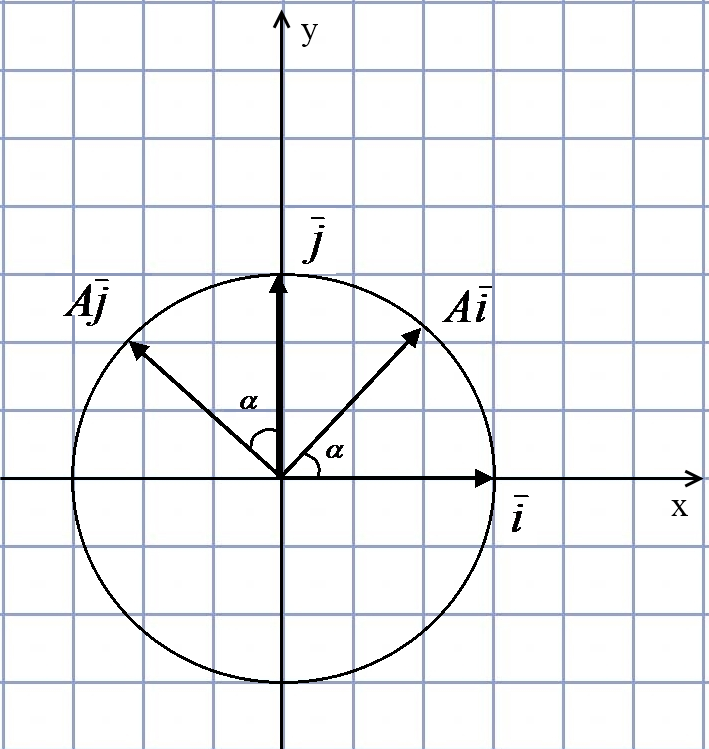
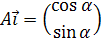
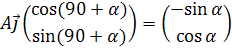
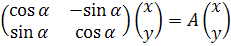
Замечание:
Матрицу поворота на угол α по часовой стрелке можно получить, подставив в предыдущую вместо α угол –α:
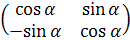
 2015-06-26
2015-06-26 1994
1994