Производная и дифференциал длины дуги

Введём переменную длину дуги

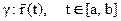S(t) – переменная длина дуги равна длине кривой от

Теорема 1

Прямая 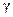- непрерывно-дифференцируемая кривая.

Тогда:

Доказательство:

По определению производной 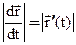Зафиксируем t₀ и дадим ей приращение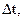 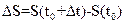, по предыдущей теореме

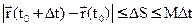
Функция 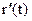непрерывна на отрезке, поэтому она достигает своего максимума, значит M – достигается в некоторой внутренней точке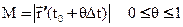

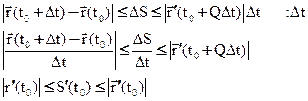по свойству непрерывности

Отсюда: