Определение. Кривые на плоскости и в пространстве

Кривые на плоскости и в пространстве

Понятие кривой

, x –действительное число элемент

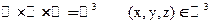
Будем рассматривать отображения из отрезка в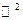

!!! образ кривой – также называют кривой

Определение

Кривая 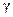- это отображение их отрезка [a, b] в 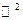(плоская кривая)

из [a, b] в 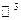(пространственная кривая)

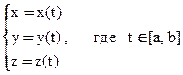
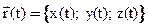- радиус вектор кривой

Одна и та же кривая может быть задана различными способами

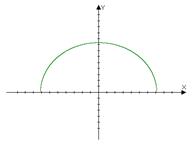
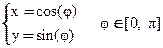
Или

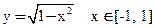
Кривая называется замкнутой, если её начало и конец совпадают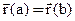

Кривая непрерывна на [a, b] если x(t), y(t), z(t) – непрерывны на этом отрезке

Кривая дифференцируема на [a, b] – если x(t), y(t), z(t) дифференцируемы внутри [a, b]

Кривая непрерывно-дифференцируема – если 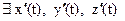и они непрерывны

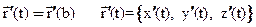
Точка кривой называется особой, если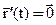

Кривая называется гладкой, если она непрерывно-дифференцируема и не имеет особых точек.

Кусочно гладкая кривая - это кривая которую можно разбить на конечное число гладких кривых.

Понятие длинны кривой и достаточное условие

спрямляемости кривой

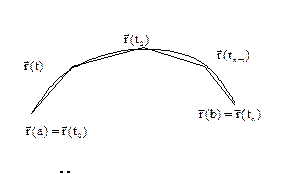Пусть 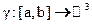, разобьём отрезок [a, b] на конечное число частей 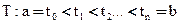- разбиение [a, b].

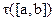- множество всех разбиений отрезка [a, b].

Разбиение отрезка [a,b] задает соответствующие разбиение на кривой. Соединим точки разбиения кривой отрезками, получим ломанную вписанную в кривую. L(T) – длина ломаной вписанной в кривую .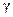

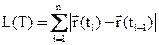
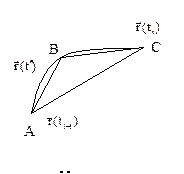Основное свойство длин вписанных ломаных: при измельчении разбиения длина ломаной не уменьшается.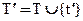

AB+BC>AC, по неравенству треугольника

Определение:

Кривая называется спрямляемой, если существует точная верхняя грань длин всех вписанных ломаных, и равна конечному числу

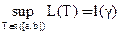- длинна кривой (! l – длинна кривой 1 - единица)

Основное свойство – аддитивность: Длина суммы двух кривых, равна сумме длин этих кривых.

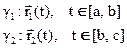
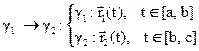сумма двух кривых неперестановочна

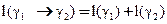
Теорема Достаточное условие спрямляемости кривой

Пусть кривая непрерывно-дифференцируема на [a, b]

Тогда:

1) 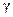- спрямляема на [a,b] то есть имеет конечную длину

2) 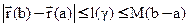, где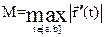

Доказательство:

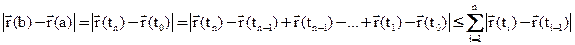
По теореме Лагранжа

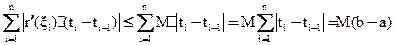
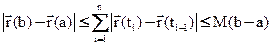Берём sup от каждой части неравенства

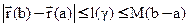
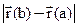- число 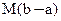- число