Кривизна кривой

Рассматриваем кривую 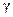заданную натуральным параметром

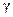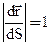
: (S), - кривая дважды дифференцируема и без особых точек - касательный вектор - единичный касательный вектор.

Зафиксируем S₀, 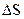- приращение

S=S₀+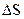

Определение

Кривизна кривой в точке S₀ - это угловая скорость вращения единичного касательного вектора

Радиус кривизны

Пример

Найдём кривизну и радиус кривизны окружности радиуса R

L=2 R

- кривизна окружности в каждой точке постоянна. Радиус кривизны совпадает с радиусом окружности.

Формулы для вычисления радиуса кривизны

- для натурального параметра

- для произвольного параметра