2015-06-28
2248
1. Сложение векторов.
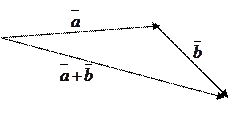
а) правило «треугольника»
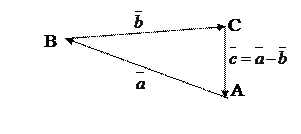
б) вычитание векторов
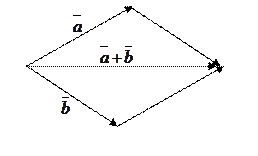
в) правило «параллелограмма»
г) правило «параллелепипеда» - для сложения трех некомпланарных векторов:
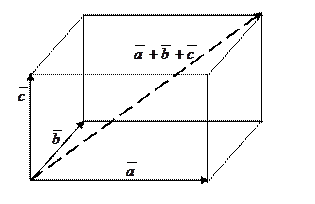Если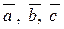 
- три ненулевых некомпланарных вектора,
то любой вектор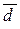 
в пространстве может быть представлен в ви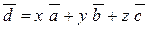де:
, где
x, y, z – единственная тройка чисел – такое равенство называется разложением вектора по некомпланарным векторам.
Некомпланарными можно считать и базисные векторы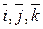 
, их координаты 
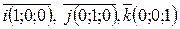, тогда получаем следующее разложение вектора по базису:
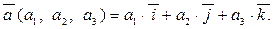
2. Умножение вектора на число.
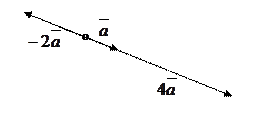
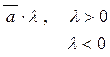
Произведением ненулевого вектор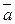а 
на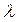 
, есть вектор 
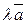, имеющий направление вектора 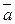, если 
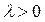, и противоположно направлен вектору 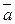, если 
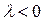; абсолютная величина этого вектора равна абсолютной величине вектора 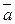, умноженной на 
.
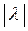| СВОЙСТВА: | |
| Сложения | Произведения на число |
1. 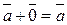 | 1.  |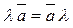
2. 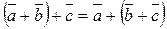 | 2.  |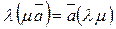
3. 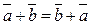 | 3.  |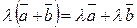
4.  |
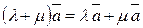Б). Векторы в прямоугольной системе координат.
Пусть 0ху – прямоугольная система координат, в которой заданы своими координатами точки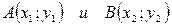 
. Тогда координатами вектора 
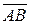будут числа 
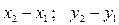, т.е.,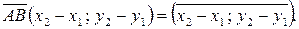 
Если 0xyz – прямоугольная система координат в пространстве, то, если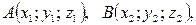 
то вектор имеет такие координаты: 
.
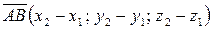Т.е., чтобы найти координаты вектора, заданного координатами своих начала и конца, надо из каждой координаты конца вектора вычесть соответствующую координату начала вектора.
