При теплообмене в связи с изменением температуры жидкости у поверхности теплоотдачи изменяются и её физические свойства, что приводит к деформации профилей скорости и температуры. При этом изменяется и коэффициент теплоотдачи. Для учета изменения физических характеристик среды от Т, а в некоторых случаях и давления, и его влияния к системе основных дифференциальных уравнений конвективного теплообмена необходимо присоединить зависимости, связывающие λ, ср,ρ, а и μ с температурой и давлением, и вся система уравнений должна решаться совместно.
Напомним, что коэффициент пропорциональности, входящий в формулу Ньютона, связывающую сдвиговое (касательное) напряжение между двумя слоями прямолинейно движущейся реальной (вязкой) жидкости с отнесенными к единице длины изменением скорости по нормали к направлению движения,
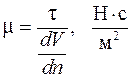 (1.198)
(1.198)
носит название динамического коэффициента вязкости.
Динамический коэффициент вязкости не зависит от характера движения потока, а определяется лишь физическими свойствами жидкости и ее температурой. В реальных жидкостях при очень больших давлениях μ может зависеть и от давления.
Кроме динамического коэффициента вязкости (или просто вязкости), используется и кинематический коэффициент вязкости
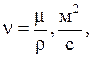 (1.199)
(1.199)
где ρ, 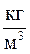 – плотность жидкости.
– плотность жидкости.
Вязкость капельных жидкостей зависит от ее химического состава, структуры молекул. В общем случае можно считать, что вязкость жидкостей практически не зависит от давления, но сильно зависит от температуры.
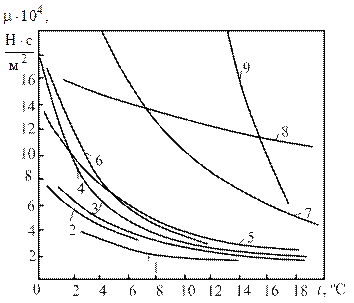
Рис. 1.2. Вязкость различных жидкостей в зависимости от температуры: 1 – метилацетат; 2 – метиловый спирт; 3 – бензол; 4 – вода; 5 – четыреххлористый углерод; 6 – этиловый спирт; 7 – дефинильная смесь (даутерм); 8 – ртуть; 9 – глицерин
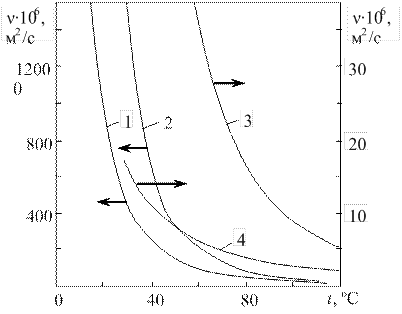
Рис. 1.3. Зависимость кинематического коэффициента вязкости различных жидкостей от температуры: 1 – масло; 2 – топочный мазут;
3 – глицерин; 4 – трансформаторное масло
С повышением температуры величина вязкости жидкостей убывает, а газов – растет. Динамический коэффициент вязкости у капельных жидкостей значительно больше, чем у газов, а кинематический коэффициент, вследствие значительно большей плотности жидкостей, меньше.
Строгой теории вязкости жидкости в настоящее время нет. Поэтому для капельной жидкостей, как и для газов, часто применяются различные эмпирические и полуэмпирические формулы зависимости их вязкости от температуры.
Наибольший интерес представляют расчетные соотношения для μ, полученные на основе зависимости вязкости от молекулярной структуры жидкости. В качестве их примера можно привести расчётную формулу Панченкова
Для газов зависимость динамического коэффициента вязкости от температуры может быть представлена формулой Саттерленда
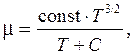 (1.202)
(1.202)
где С – постоянная Саттерленда; для воздуха С ≈ 122.
Величина плотности зависит от природы жидкости (рис. 1.2) (от ее молекулярного строения) и является функцией давления и температуры, т.е.
ρ = ρ (р, Т) (1.206)
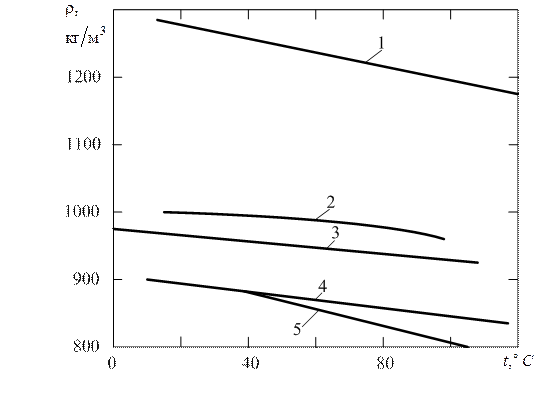
Рис. 1.4 Зависимость плотности различных жидкостей от температуры: 1 – глицерин; 2 – вода; 3 – топочный мазут-40; 4 – масло МС-20;
Плотность капельных жидкостей с ростом давления изменяется мало. Плотность газов, наоборот, при постоянной температуре возрастает практически прямо пропорционально росту давления.
Зависимость плотности от температуры для капельных жидкостей и газов также различна.
Изменение плотности жидкости от температуры, как уже отмечалось выше, характеризуется коэффициентом объёмного расширения
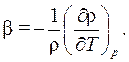 (1.207)
(1.207)
Величина β для жидкостей меньше, чем для газов. Для капельных жидкостей β от Т изменяется мало.
При расчетах используют линейные зависимости плотности от температуры вида:
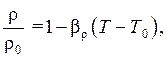 (1.208)
(1.208)
Плотность идеального (совершенного) газа может быть определена по уравнению состояния Клапейрона
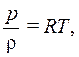 (1.210)
(1.210)
где R – универсальная постоянная.
Известно, что теплопроводность жидкостей является следствием передачи энергии соударения молекул между собой и переносом ее диффундирующими молекулами. Теплопроводность жидкостей зависит от их рода, температуры и давления. Коэффициент теплопроводности λ изменяющийся для различных жидкостей (рис. 1.5) в диапазоне от 0,007 до 0,7 Вт/(м∙К).
Существуют эмпирические уравнения, связывающие λ жидкостей с температурой.
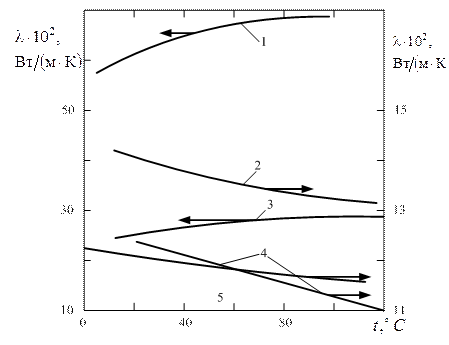
Рис. 1.5 Зависимость коэффициента теплопроводности различных жидкостей от температуры: 1 – вода; 2 – масло МС-20; 3 – глицерин; 4 – трансформаторное масло; 5 – топочный мазут-40
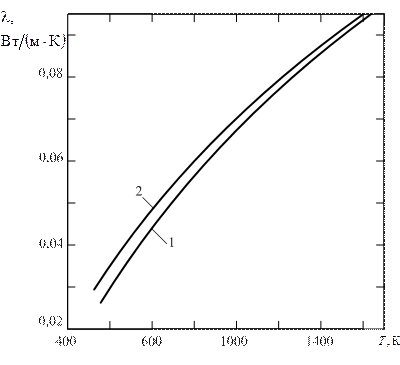
Рис. 1.6 Коэффициент теплопроводности воздуха при:
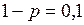 МПа, 2 – 5,0
МПа, 2 – 5,0
С увеличением температуры 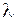 жидкости, за исключением воды и глицерина, уменьшается (рис. 1.5). С ростом давления
жидкости, за исключением воды и глицерина, уменьшается (рис. 1.5). С ростом давления 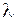 увеличивается незначительно.
увеличивается незначительно.
Изменение 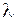 воздуха в зависимости от температуры показано на рис. 1.6.
воздуха в зависимости от температуры показано на рис. 1.6.
На рис. 1.7 приведены значения теплоёмкости различных жидкостей при постоянном давлении в зависимости от температуры. Изменение теплоёмкости воздуха в зависимости от температуры и давления показано на рис. 1.8.
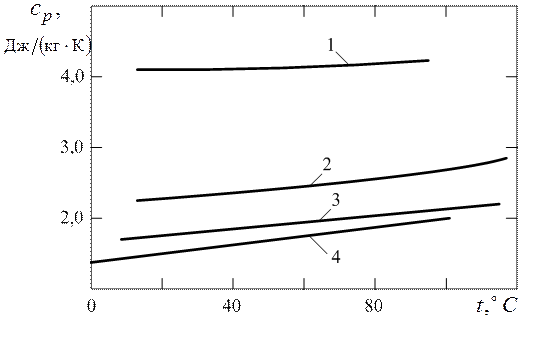
Рис. 1.7 Теплоёмкость различных жидкостей в зависимости от температуры: 1 – вода; 2 – глицерин; 3 – масло МС-20; 4 – топочный
мазут-40 и трансформаторное масло
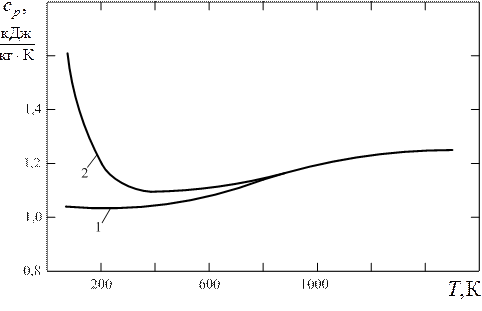
Рис. 1.8 Теплоёмкость 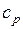 воздуха при
воздуха при 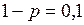 МПа;
МПа;
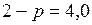 МПа
МПа
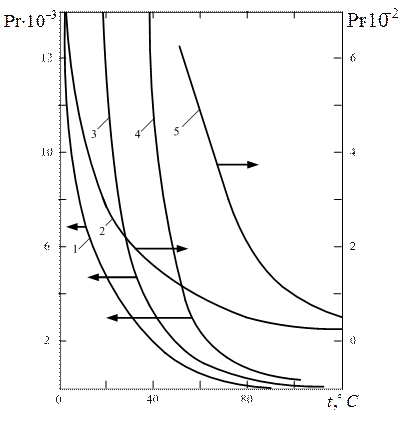
Рис. 1.9 Число Pr различных жидкостей в зависимости от температуры: 1 – вода; 2 – трансформаторное масло; 3 – масло МС-20; 4 - топочный мазут; 5 - глицерин
Одной из важных характеристик, представляющих теплофизические свойства теплоносителя, является число Прандтля
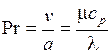 . (1.215)
. (1.215)
Число Прандтля жидкостей больше единицы и изменяется в очень широком диапазоне в зависимости от температуры. Причём характер зависимости числа Pr от температуры аналогичен изменению кинематического коэффициента вязкости или просто вязкости (рис. 1.9).
Число Pr газов зависит от их атомности. В соответствии с кинетической теорией газов, величина Pr изменяется от 0,67 до 1 при числе атомов в молекуле газа от 1 до 4.
Число Pr газов слабо зависит от температуры теплоносителя (рис. 1.10)
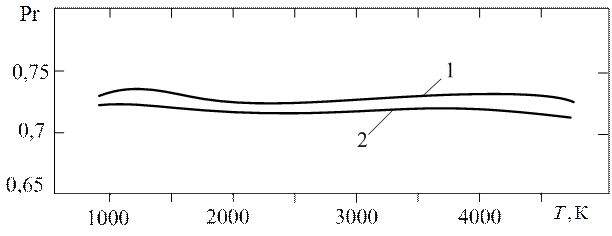
Рис. 1.10. Зависимость числа Pr от температуры
для воздуха (1) и азота (2)
Зависимость числа Pr газов от их атомности имеет вид
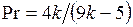 , (1.216)
, (1.216)
где 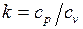 - функция атомности газа; для одного, двух, трёх и более атомных газов k = 1,67; 1,4; 1,29 и 1,33 соответственно.
- функция атомности газа; для одного, двух, трёх и более атомных газов k = 1,67; 1,4; 1,29 и 1,33 соответственно.
Поправки для учёта переменности физических параметров вводимые в уравнения подобия представляют часто в виде безразмерных соотношений 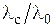 ,
, 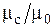 ,
, 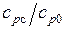 , где индексы «с» и «0» обозначают, что физическая характеристика определяется по температуре поверхности теплоотдачи (стенки) или по температуре внешнего (невозмущённого) потока T 0.
, где индексы «с» и «0» обозначают, что физическая характеристика определяется по температуре поверхности теплоотдачи (стенки) или по температуре внешнего (невозмущённого) потока T 0.
Для капельных жидкостей удовлетворительную связь между числами Нуссельта и коэффициентами сопротивления трения при неизменных (постоянных) физических характеристиках (Nuн и cf н) и переменными (Nu и cf) дают уравнения:
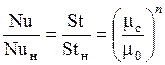 , (1.217)
, (1.217)
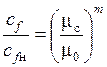 . (1.218)
. (1.218)
Показатели m и n зависят от геометрических параметров системы и характера течения. В задачах конвективного теплообмена при вынужденном движении они зависят и от диапазона чисел Рейнольдса.
Экспериментально установлено, что при турбулентном и при ламинарном режимах, влияние переменности физических свойств жидкости на теплоотдачу можно учесть введением в расчётное уравнение поправки 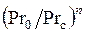 . Для большинства практически важных случаев как при охлаждении, так и при нагревании жидкости в инженерных расчётах можно принять
. Для большинства практически важных случаев как при охлаждении, так и при нагревании жидкости в инженерных расчётах можно принять 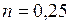 . В действительности при нагревании жидкости влияние переменности физических свойств больше, чем при охлаждении. Так, при нагреве
. В действительности при нагревании жидкости влияние переменности физических свойств больше, чем при охлаждении. Так, при нагреве 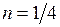 , а в случае охлаждения жидкостей с
, а в случае охлаждения жидкостей с 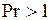
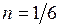 или
или 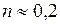 . Заметим, что множитель
. Заметим, что множитель 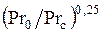 был предложен М.А. Михеевым. Поправка
был предложен М.А. Михеевым. Поправка 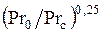 на газы не распространяется. Зависимость n от числа Рейнольдса незначительна.
на газы не распространяется. Зависимость n от числа Рейнольдса незначительна.
Таким образом, расчётное обобщённое уравнения теплоотдачи при рассмотренном способе учёта переменности физических свойств жидкости примет вид
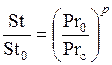 . (1.219)
. (1.219)
Зависимости 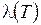 ,
, 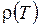 и
и 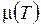 при умеренных температурах для различных газов подобны, поэтому влияние зависимости физических свойств газов от температуры на теплообмен и сопротивление можно учесть по уравнениям:
при умеренных температурах для различных газов подобны, поэтому влияние зависимости физических свойств газов от температуры на теплообмен и сопротивление можно учесть по уравнениям:
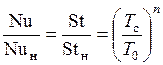 ; (1.220)
; (1.220)
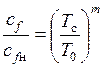 . (1.221)
. (1.221)
Отношение 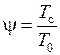 - абсолютной температуры газа на поверхности тела (или на стенке
- абсолютной температуры газа на поверхности тела (или на стенке 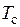 ) к характерной абсолютной температуре потока (
) к характерной абсолютной температуре потока (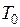 ) называется температурным фактором (temperature ratio parameter).
) называется температурным фактором (temperature ratio parameter).
При турбулентном течении в круглой трубе газа, у которого зависимость физических свойств от температуры такая же, как у воздуха, можно рекомендовать следующие значения n и m в формулах (1.220) и (1.221):
при 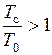 (нагревание газа)
(нагревание газа) 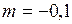 ;
; 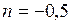 ;
;
при  (охлаждение газа)
(охлаждение газа) 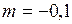 ;
; 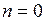 .
.
 2015-06-28
2015-06-28 883
883








