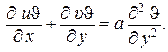Последний член равенства (1.279) по условию сплошности равен нулю. Тогда уравнение (1.274) представим так

(1.280)

Уравнение неразрывности может быть записано в виде

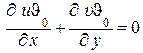. (1.281)

Вычтем из уравнения (1.228) уравнение (1.227), в результате получим

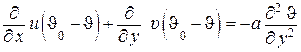. (1.282)

Учитывая, что

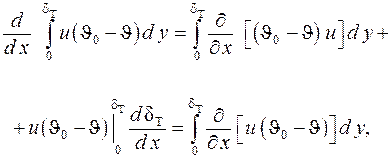(1.283)

интегрируем уравнение (1.282) от нуля до δ_Т (или до бесконечности), в результате получаем

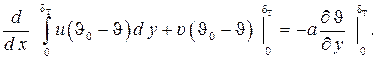(1.284)

Второй член левой части полученного равенства равен нулю, т.к. в соответствии с граничными условиями при y = 0 υ = 0, а при 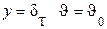. Поэтому можем записать

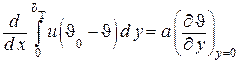. (1.285)

Преобразуем подынтегральное выражение уравнения (1.285), умножив и разделив его на . В результате уравнение (1.285) примет вид

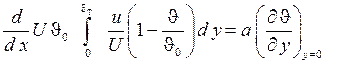. (1.286)

Вводим в рассмотрение толщину потери энтальпии. После дифференцирования и элементарных преобразований (1.286) находим

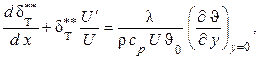(1.287)

где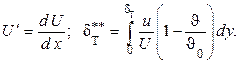

При безградиентном течении 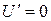, поэтому полученное интегральное соотношение (1.287) может быть записано так

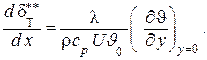(1.287)

Учитывая, что

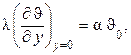
можем записать

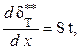(1.289)

где

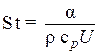(1.290)

есть число Стантона (Stanton number).

Итак, для безградиентного течения жидкости интегральное соотношение для теплового пограничного слоя имеет вид (1.289).

Интегральное соотношение для теплового пограничного слоя может быть получено и из рассмотрения контрольной поверхности, ограничивающей элементарный объем жидкости, заключенный между двумя бесконечно близко расположенными сечениями теплового пограничного слоя, т.е. тем же методом, который был использован в гидромеханике для вывода уравнения импульсов.

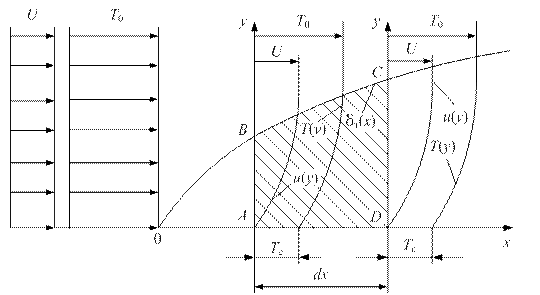
Рис. 1.13. К выводу интегрального соотношения для теплового пограничного слоя

Контрольная поверхность в виде контура ABCD ограничивает выделенный бесконечно малый контрольный объём. Считаем, что толщина теплового пограничного слоя в сечении AB равна δ_Т (AB = δ_Т).

Массовый расход теплоносителя через грань AB контура ABCD в единицу времени составит

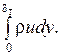(1.291)

Одновременно вместе с массой через грань AB передаётся в единицу времени количество теплоты (энтальпии)

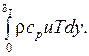(1.292)

Изменение количества теплоты на единицу длины составит

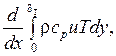(1.293)

а на расстоянии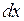

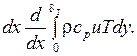(1.294)

Последняя формула определяет количество теплоты переносимое в единицу времени через грань контрольного элемента CD.

Количество теплоты поступающее вместе с ней через BC найдём по выражению

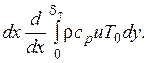(1.295)

Количество теплоты, переданное через AD, равно

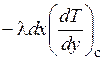или 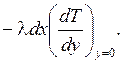(1.296)

При ρ = const, c_p = const и λ = const

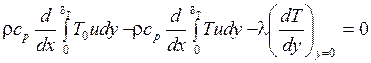(1.297)

или

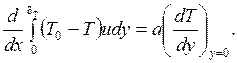(1.298)

Если полученное уравнение записать, введя в рассмотрение избыточную температуру 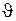= T – T _c, то оно примет вид полностью совпадающий с (1.285)

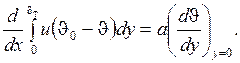(1.299)

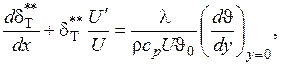(1.300)

При безградиентном течении 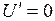поэтому интегральное соотношение (1.300) примет вид

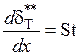. (1.301)

Уравнения (1.300) и (1.301) совпадают с ранее полученными уравнениями (1.287) и (1.289) соответственно.

Применительно к двухмерному турбулентному пограничному слою уравнение энергии может быть упрощено (считаем, что ось y перпендикулярна поверхности теплоотдачи) и в результате оценки членов записано в виде

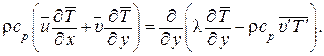(1.302)

Из уравнения (1.302) следует, что полный тепловой поток через турбулентный пограничный слой состоит из суммы двух тепловых потоков, обусловленных молекулярным и турбулентным механизмами переноса.

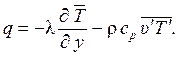(1.303)

Плотность турбулентного теплового потока

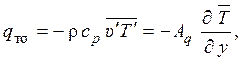(1.304)

где 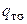– плотность турбулентного теплового потока; A_q – коэффициент турбулентного переноса теплоты (eddy diffusivity of heat transfer) или коэффициент турбулентной теплопроводности – величина, характеризующая интенсивность турбулентного переноса теплоты.

Из формулы (1.304) видно, что

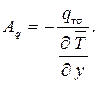(1.305)

Величина

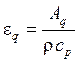(1.306)

носит название кинематического коэффициента переноса теплоты (eddy thermal diffusivity) или коэффициента турбулентной температуропроводности.

Используя ε _q можно 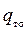определить следующим образом:

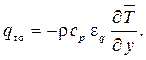(1.307)

Отношение кинематического коэффициента турбулентного переноса количества движения 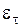к кинематическому коэффициенту переноса теплоты ε _q называют турбулентным числом Прандтля (turbulent Prandtl number),

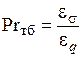. (1.308)

По определению турбулентное число Прандтля определяет различие между переносами импульса и теплоты.

Турбулентные аналоги коэффициентов λ и а не зависят от физических свойств среды, а определяются лишь координатами точки в пространстве и скоростью движения потока (градиентом скорости).

Таким образом, уравнение (1.303) можно записать следующим образом:

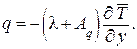(1.309)

или

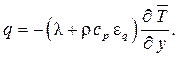(1.310)

Уравнение энергии для двухмерного турбулентного пограничного слоя с учетом полученных соотношений имеет вид

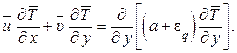(1.311)

Уравнение движения турбулентного пограничного слоя может быть получено из уравнений осредненного турбулентного движения (уравнений Рейнольдса). Так, для стационарного двухмерного безградиентного движения

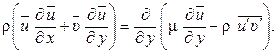(1.312)

С введением в рассмотрение коэффициента турбулентной вязкости или коэффициента турбулентного переноса количества движения (eddy diffusivity of momentum)

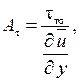(1.313)

где 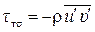– турбулентное касательное напряжение. По формуле Прандтля

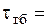
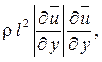(1.313)

где l – путь смешения, .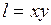

Поэтому

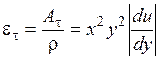. (1.315)

Тогда уравнение (1.312) можно представить в виде

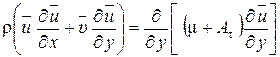(1.316)

или

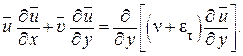(1.317)

Формулы (1.307) и (1.310) позволяют найти соотношение между плотностями теплового потока, обусловленными турбулентным и молекулярным переносом теплоты

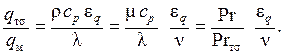(1.318)

В технических расчетах часто полагают 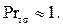Отношение ε_τ/ v зависит от координат рассматриваемой точки потока и числа Pr и не зависит от рода жидкости. Поэтому из соотношения (1.317) следует, что роль турбулентного переноса существенно зависит от числа Pr. Она более существенна в средах с большими значениями числа Прандтля. В этих случаях для правильного расчета теплообмена необходимо точное знание изменения отношения ε_τ/ v. При больших значениях Pr термическое сопротивление сосредоточено преимущественно в подслое. При очень низких числах Прандтля (жидкие металлы), наоборот, молекулярная теплопроводность определяет процесс теплопереноса не только в ламинарном подслое, но даже и в турбулентном ядре. Термическое сопротивление распределено по всему сечению потока.

Следует заметить, что в расчетах обычно коэффициент турбулентного переноса теплоты выражают через коэффициент турбулентного переноса количества движения. В этом случае плотность теплового потока в соответствии с уравнениями (1.310) и (1.318) представляют в виде

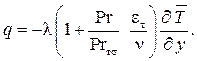(1.319)

В настоящее время для наиболее практически важных случаев турбулентных течений разработан ряд рекомендации по определению отношения ε_τ/ v. Использование их позволяет замкнуть систему уравнений и получить в ряде случаев в расчетах вполне удовлетворительные результаты.

На рис. 1.15 сопоставлены относительные коэффициенты 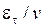по формулам Прандтля, Рейхардта и Дайслера в пристеночной зоне при 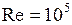. Из рисунка видно, что в большей части потока турбулентный перенос намного интенсивней молекулярного, отношение 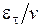достигает нескольких сотен.

Кривая 1, соответствующая двухслойной схемы Прандтля и трёхслойной схеме Кармана, является приближённой аппроксимацией действительных распределений .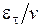

Для описания распределения скорости в турбулентном ядре потока, как отмечалось в курсе гидромеханики, широко используется степенная зависимость вида

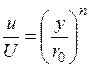, (1.329)

где показатель степени n в общем случае зависит от числа Рейнольдса.

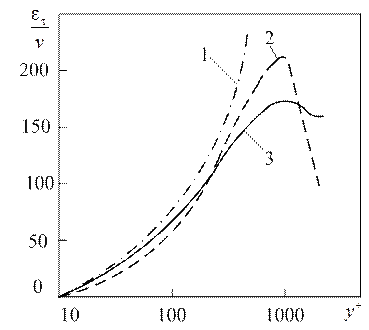
Рис. 1.15. Распределения 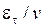в круглой цилиндрической трубе:

1 – по Прандтлю и Карману; 2 – по Дайслеру; 3 – по Рейхардту

* Под термином «трубы» здесь и в дальнейшем понимаются трубы (или закрытые по всему периметру каналы) произвольного, но постоянного по длине поперечного сечения, в которых осуществляется напорное течение жидкости.

* Росби (Rossby) Карл Густав Арвид (1898-1957) – швед. Труды по динамике и термодинамике атмосферных процессов и атмосферной турбулентности.

** Кориолис (Coriolis) Гюстав Гаспар (1792-1843) – французский учёный в области механики. Труды по теории относительного движения, ввёл понятия силы и ускорения Кориолиса.

* Фруд (Froude) Вильям (1810 – 1879) – английский инженер, создатель классической методики модельных испытаний. Выполнил большое количество работ по изучению гидродинамического сопротивления, качки, устойчивости и маневренности судов, работы гребного винта.

* Эйлер Леонард (1707 – 1783) - математик, механик, физик и астроном. По происхождению швейцарец. В 1727 г. переехал в Россию. Академик Петербургской АН с 1766 г. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математике, физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавшим значительное влияние на развитие мировой науки. Член практически всех ведущих научных академий и обществ.

* Лагранж (Lagrange) Жозеф Луи (1736-1813) – французский математик и механик, член (1759) и президент (1766-1787) Берлинской АН, иностранный почётный член Петербургской АН (1776). Труды по вариационному исчислению, математическому анализу, теории числе, алгебре, дифференциальным уравнениям.