2015-06-28
875
Отклонением точки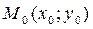 
от прямой L называется расстояние от этой точки до прямой L, взятое со знаком “+”, если точка 
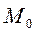и начало координат O находятся по разные стороны от прямой L, и со знаком “–”, если 
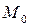и O находятся по одну сторону от L. Если O лежит на L, то знак не определен.
Теорема 2 (об отклонении точки от прямой).
Пусть уравнение прямой L имеет вид (27), тогда отклонение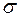 
произвольной точки плоскости 
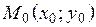от этой прямой равно 
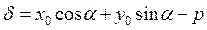(29)
Д-во:
, 
, 
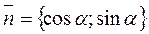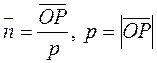
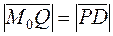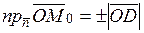
Докажем, что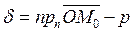 
1. 
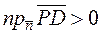
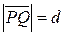- расстояние от 
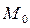до L.
L разделяет плоскость на две полуплоскости, а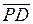 
направлен в ту полуплоскость, где находится точка 
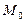. Если 
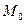и O находятся по разные стороны от L, то 
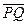сонаправлен с вектором 
.
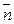2. 
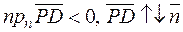, тогда 
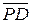направлен в ту полуплоскость, где находится точка O, т.е. 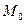и О находятся по одну сторону от прямой L.
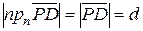
Следовательно, по определению отклонения из п.п. 1 и 2 вытекает, что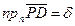 
Вычислим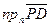 
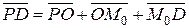
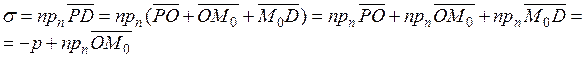
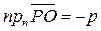
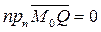
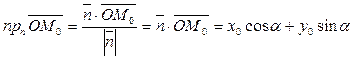
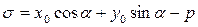
Теорема доказана
Следствие: Расстояние от точки 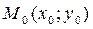допрямой L, заданной нормированным уравнением равно
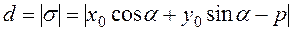(30)
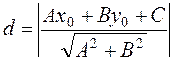(31)
Пример:
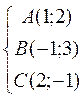
Найти:
1) высоту h в треугольнике ABC, опущенную из вершины A;
|
|
|
2) уравнение биссектрисы внутреннего угла B.
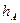- расстояние от точки A до прямой BC.
1. 
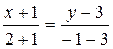
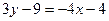
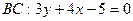
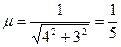
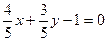
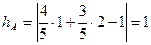
2. 
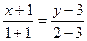
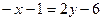
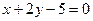
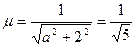
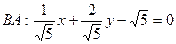
Пусть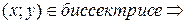 
расстояния от т. M (x; y) до прямых BA и BC равны между собой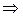 
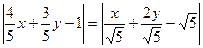
а)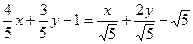 
б)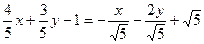 
а)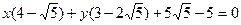 
б)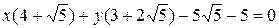 
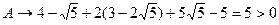
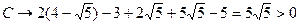
нам нужно уравнение б).
