Переход от общего уравнения прямой к нормированному

Пусть прямая L не проходит через начало координат в ПДСК. Опустим из начала координат перпендикуляр на прямую L и пусть основанием этого перпендикуляра будет точка Р.

Обозначим

.

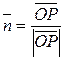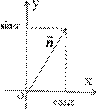Вектор 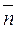всегда направлен от начала координат к прямой. Он является единичным нормальным вектором прямой.

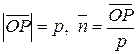
р – расстояние от начала координат до прямой L.

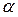- угол наклона 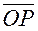к оси 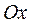, т.к. ,

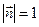то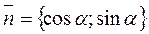

Пусть M – текущая точка на прямой L; 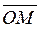- радиус-вектор точки M.

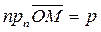(26)

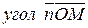- острый всегда

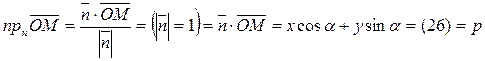
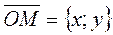
Тогда из (26) вытекает уравнение

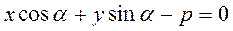(27)

(27)- нормированное (нормальное) уравнение прямой.

Приведение общего уравнения прямой

к нормированному виду

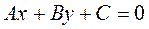(2)

Рассмотрим число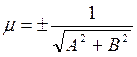

Умножим на μ уравнение (2):

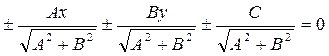
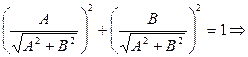
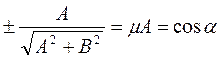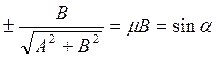, (28)

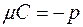
p – расстояние от начала координат до прямой .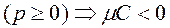

Знак 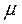выбираем противоположно знаку C.