Взаимное расположение плоскостей определяется их нормальными векторами.
Пусть 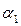 ,
, 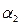 заданы своими общими уравнениями:
заданы своими общими уравнениями:
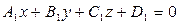
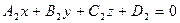
Условие параллельности плоскостей
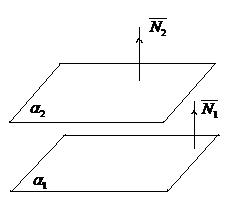 Рис.6 Рис.6 | Если 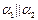 , то , то 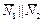 (рис.6). Запишем условие параллельности векторов: - в векторной форме: (рис.6). Запишем условие параллельности векторов: - в векторной форме: 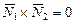 - в координатной форме: - в координатной форме: 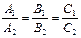 (5) (5) |
1.8.2 Условие перпендикулярности плоскостей
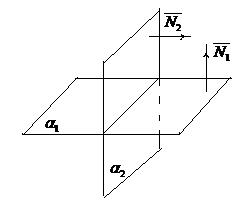 Рис.7 Рис.7 | Если 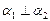 , то , то 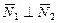 (рис.7). Запишем условие перпендикулярности векторов: в векторной форме: (рис.7). Запишем условие перпендикулярности векторов: в векторной форме: 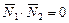 в координатной форме: в координатной форме: 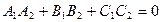 (6) (6) |
Угол между плоскостями
Угол между плоскостями определяется углом между их нормальными векторами
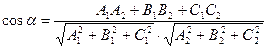 (7)
(7)
 2015-06-28
2015-06-28 1161
1161








