2015-06-28
11788
Задача 4 Составить уравнение плоскости, проходящей через начало координат и точк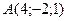и: 
и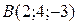 
Решение
Начало координат, точка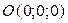 
Воспользуемся уравнением плоскости, проходящей через три точки
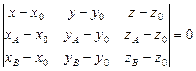
Подставим координаты точек, получим: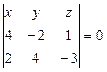 
Имеем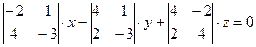 
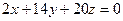
Разделим оби части уравнения почленно на 2, получим
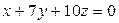
Ответ: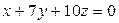
Замечание При составлении уравнения плоскости, проходящей через три точки можно воспользоваться «основным» уравнением плоскости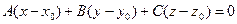 
, действительно, если точк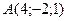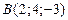и , 
и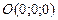 
лежат в одной плоскости (рис.9), то векторы 
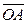и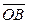 
перпендикулярны вектору 
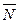, тогда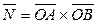 
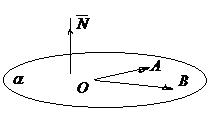
Рис.9
Если векторы 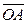и 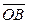выходят из начала координат (радиусы - векторы) то их координаты совпадают с координатами конца, т.е.
, 
.
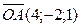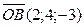Найдем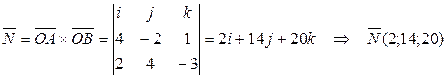 
.
В качестве точки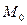 
можно взять любую из точек 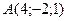, 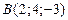или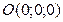 
.
Возьмем точку 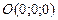, получим
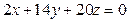
Разделим оби части уравнения почленно на 2, получим
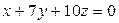
Ответ: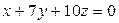
Задача 5 Составить уравнение плоскости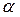 
, проходящей через точк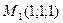и 
и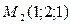 
параллельно вектору 
.
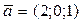Решение
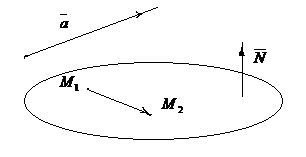
Рис.10
Выполним схематичный чертёж (рис. 10).
|
|
|
1 Плоскость проходит через точку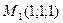
2 Вектор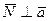 
по условию, 
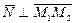, т.к. 
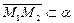. Векторы 
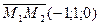и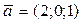 
неколлинеарные, тогда 
.
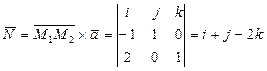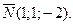
3Составим уравнение плоскости, используя уравнение (1), получим
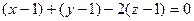или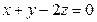 
Замечание Так как в последнем уравнении отсутствует свободный член, то плоскость проходит через начало координат.
Ответ: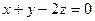 
Задача 6 Составить уравнение плоскости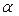 
, проходящей через точку 
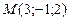параллельно плоскости 
: 
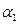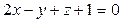
Решение
1 По условию дана точка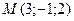 
через которую проходит плоскость .
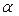2 По условию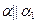 
, тогда 
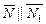, поэтому в качестве вектора 
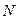(нормального вектора искомой плоскости 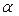) можно взять 
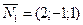- нормальный вектор данной плоскости .
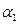3 Составим уравнение плоскости 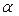используя уравнение (1)
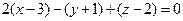
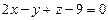
Ответ: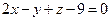 
Задача 7 Составить уравнение плоскости 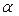, проходящей через ось OZ и точку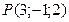 
Решение
СПОСОБ 1
1Плоскость проходит через ось OZ, тогда её уравнение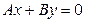 
(см. таблицу 2)
2 Точка 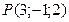принадлежит плоскости, её координаты удовлетворяют уравнению плоскости, имеем 
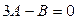. Выразим В через А: В=3А и подставим у уравнение плоскости
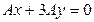, сократим на А, получим 
.
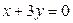СПОСОБ 2
Выполним схематичный чертёж (рис. 11).
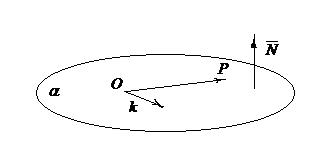Рис.11
1 Плоскость 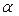проходит через точку .
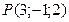2 По условию плоскость 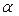проходит через ось OZ, значит орт 
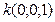лежит в плоскости .
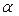Рассмотрим вектор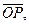 
т.к это радиус-вектор то его координаты совпадают с координатами конца, т.е. точки .
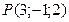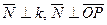, тогда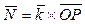 
, 
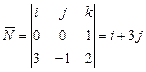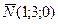
3 Составим уравнение плоскости 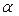используя уравнение (1)
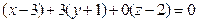, или
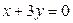
Ответ: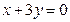 
Задача 8 Написать уравнение плоскости 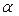, проходящей через точку 
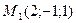и 
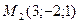перпендикулярно плоскости 
.
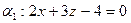Решение
Выполним схематичный чертёж (рис. 12).
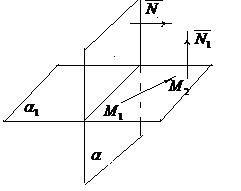
Рис.12
1 Плоскость 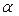проходит через точку .
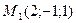2 Найдем нормальный вектор плоскости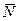 
|
|
|
По условию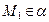 
и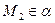 
, отсюда следует, что 
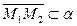и 
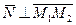
Плоскост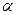и 
и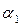 
перпендикулярны, значит 
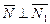, тогда 
.
, 
, 
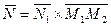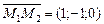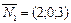
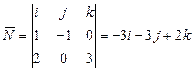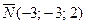
3 Составим уравнение плоскости 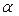используя уравнение (1)
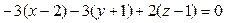
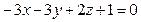, или
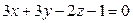
Ответ: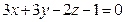 
Задача 9 Вычислить объём пирамиды, ограниченной плоскостью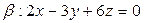 
и координатными плоскостями.
Решение
1 Найдём отрезки, которые плоскость отсекает на осях координат. Запишем уравнение плоскости в отрезках (3)
,
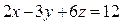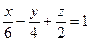
2Обозначим точки пересечения с осями координат OX, OY, OZ, соответственно A, B, C, тогда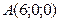 
, 
, 
.
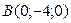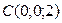3 Рассмотрим векторы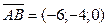 
и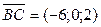 
и найдём площадь основания пирамиды (ABC), используя геометрический смысл векторного произведения:
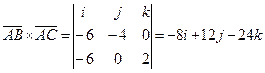
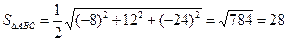(кв.ед.)
Составить уравнение плоскости (ABC):
,
,
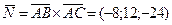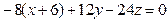разделим почленно обе части уравнения на (– 4), получим:
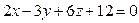
Длину высоты пирамиды найдём как расстояние от начала координат до плоскости (ABC)
по формуле вычисления расстояния от точки до прямой
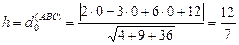
Используя формулу вычисления объёма пирамиды из курса стереометрии, найдём объём
пирамиды:
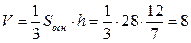(куб.ед.)
Ответ: 8 (куб.ед.)
