Уравнение плоскости, проходящей через три точки

1 Дано:

,

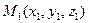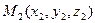
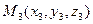
(М₁,М₂,М₃) 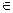α

______________________

Составить уравнение плоскости α

2 Выполним схематичный чертёж (рис. 5).

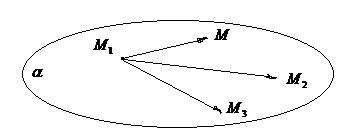
Рис.5

3 Выберем произвольную точку М(х,у,z) принадлежащую плоскости α.

4 Составим математическую модель задачи

Точки 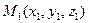, , 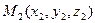, 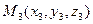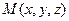принадлежат плоскости, тогда векторы: 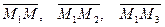(обратите внимание, что вектора рассматриваются из одной точки М₁) также лежат в одной плоскости по аксиоме: если две точки прямой лежат в плоскости, то все точки прямой лежат в плоскости. Если три вектора лежат в одной плоскости, то они компланарные (по определению).

Если вектора компланарные, то их смешанное произведение равно нулю, тогда имеем:

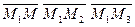() = 0 (***).

Получили уравнение плоскости в векторной форме.

5 Запишем, полученное уравнение (***) плоскости в координатной форме.

Найдем координаты векторов: , ,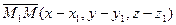

.

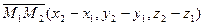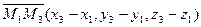Запишем смешанное произведение в координатной форме

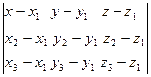= 0 (4)

Задача 2 Составить уравнение плоскости, проходящей через три точки: А(1, -6, 7),

В(4,5,-3) и С(3,0,2).

Решение

Используя уравнение (4), запишем искомое уравнение в виде:

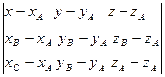= 0

Подставим координаты точек, получим

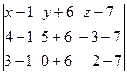= 0

Выполним вычисления, получим

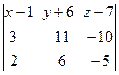= 0

Разложим определитель по элементам первой строки, получим

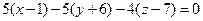
Приведем уравнение к общему уравнению плоскости

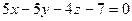
Ответ: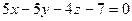

Основные уравнения плоскости представлены в структурной схеме 1