Таблица 3
| № | Базовые уравнения, формулы и понятия | Аналитический вид уравнений, формул и понятий |
| Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору («основное») | 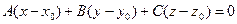 | |
| Общее уравнение плоскости | 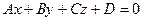 , где А, В, С координаты нормального вектора , где А, В, С координаты нормального вектора 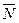 , , 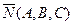 | |
| Уравнение плоскости в «отрезках» | 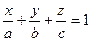 | |
| Уравнение плоскости, проходящей через три точки: А, В, С. | 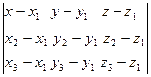 = 0 = 0 | |
Взаимное расположение плоскостей: 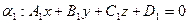 , , 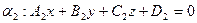 | ||
| 5.1 | Условие параллельности плоскостей в векторной форме | 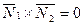 |
| 5.2 | Условие параллельности плоскостей в координатной форме | 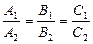 |
| 5.3 | Условие перпендикулярности плоскостей в векторной форме | 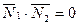 |
| 5.4 | Условие перпендикулярности плоскостей в координатной форме | 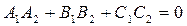 |
| Угол между плоскостями | 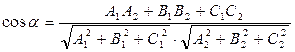 | |
Расстояние от точки 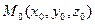 до плоскости до плоскости 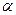 : : 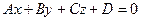 | 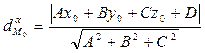 | |
| Общее уравнение прямой | 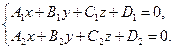 | |
| Канонические уравнения прямой | 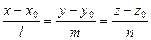 | |
| Параметрические уравнения прямой | 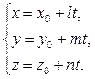 | |
Уравнения прямой, проходящей через две точки 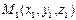 и и 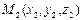 | 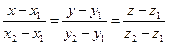 |
 2015-06-28
2015-06-28 799
799








