Две теоремы о проекции вектора на ось

Теорема 1. Проекция вектора на ось равна произведению длины этого вектора на косинус угла между рассматриваемой осью и вектором, т.е.

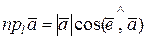
где - рассматриваемая ось, 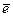- орт оси .

Доказательство теоремы предлагаем провести самостоятельно.

Теорема 2. Проекция вектора на числовую ось равна разности координат проекций конца и начала этого вектора на ту же ось, т. е.

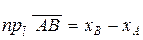
где 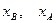- соответственно координаты проекций начала и конца вектора 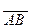на числовую ось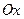

Доказательство. Обозначим проекции начала и конца рассматриваемого вектора 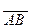на числовую ось 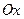соответственно через 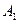и .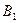

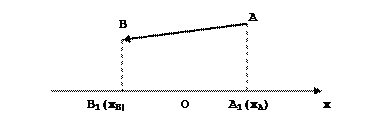
Возможны шесть случаев взаимного расположения точек 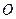, , 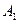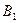на оси 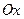. Проведем доказательство применительно к случаю, указанному на чертеже. Согласно определению проекции вектора на ось, применительно к чертежу,

.

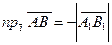Очевидно, что в рассматриваемом случае .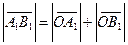

Кроме того, по определению координаты точки на числовой ос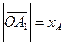и, и 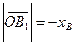. Следовательно, 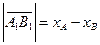, и потому .

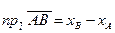Для других возможных случаев взаимного расположения точек 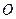, , 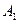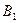на числовой оси 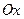доказательство теоремы предлагаем провести самостоятельно.

Аналогично можно показать справедливость равенств

,

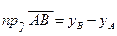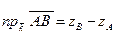
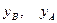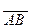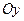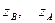где - соответственно координаты проекций начала и конца вектора на числовую ось и - соответственно координаты проекций начала и конца вектора 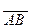на числовую ось .

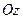В декартовой системе координат 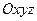числа 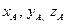и числа 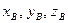- соответственно координаты точек 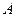и 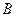. Из вышеизложенного следует утверждение:

проекция вектора на координатную ось равна разности соответствующих одноименных координат конца и начала этого вектора.