1. Векторное произведение двух векторов обладает свойством антипереместительности:
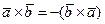 .
.
Доказательство. Для того, чтобы доказать, что векторы 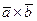 и
и 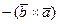 равны, докажем, что равны их проекции на любую ось. Пусть
равны, докажем, что равны их проекции на любую ось. Пусть  - произвольная ось. По свойству 3 скалярного произведения двух векторов
- произвольная ось. По свойству 3 скалярного произведения двух векторов
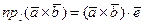 ,
,
где 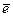 - орт оси
- орт оси  . С учетом свойства 3 смешанного произведения трёх векторов это равенство принимает вид
. С учетом свойства 3 смешанного произведения трёх векторов это равенство принимает вид
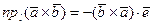 .
.
Если же теперь в правой части применить свойства 3 и 4 скалярного произведения двух векторов, то получим 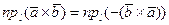 , где
, где  - любая ось.
- любая ось.
Следовательно, согласно критерию равенства двух векторов 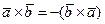 .
.
2. Скалярный множитель можно вынести за знак векторного произведения двух векторов:
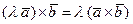 и
и 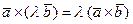
Доказательство. Убедимся в справедливости первого равенства. Для этого достаточно доказать, что 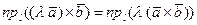 где
где  - любая ось. По свойству 3 скалярного произведения двух векторов
- любая ось. По свойству 3 скалярного произведения двух векторов
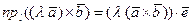 ,
,
где 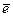 - орт оси
- орт оси  . С учетом свойства цикличности смешанного произведения трёх векторов это равенство принимает вид
. С учетом свойства цикличности смешанного произведения трёх векторов это равенство принимает вид
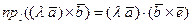 ,
,
или, в силу свойства 4 скалярного произведения двух векторов,
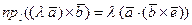 .
.
Если же в правой части этого равенства вновь воспользоваться свойством цикличности смешанного произведения трёх векторов и свойством 3 скалярного произведения двух векторов, то имеем
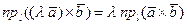 .
.
Учитывая теорему о проекции на ось произведения вектора на скаляр, получим
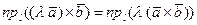
где  - любая ось, и потому, согласно критерию равенства двух векторов,
- любая ось, и потому, согласно критерию равенства двух векторов,
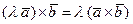 .
.
Аналогично можно доказать справедливость второго равенства.
3. Векторное произведение двух векторов обладает свойством распределительности, то есть
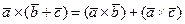 .
.
Доказательство. Докажем, что 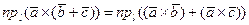 где
где  - произвольная ось. По свойству 3 скалярного произведения двух векторов
- произвольная ось. По свойству 3 скалярного произведения двух векторов
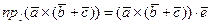 ,
,
где 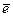 - орт оси
- орт оси  . С учетом свойства цикличности смешанного произведения трех векторов это равенство принимает вид
. С учетом свойства цикличности смешанного произведения трех векторов это равенство принимает вид
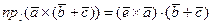 .
.
В силу свойства распределительности скалярного произведения двух векторов имеем
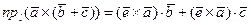 .
.
В каждом слагаемом правой части последнего равенства вновь применим свойство цикличности смешанного произведения трех векторов. Тогда получим
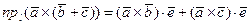 ,
,
или, с учетом свойства распределительности скалярного произведения,
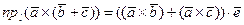 .
.
Если же ещё раз воспользоваться свойством 3 скалярного произведения двух векторов, то придем к выводу, что
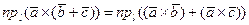
где  - любая ось, и потому, согласно критерию равенства двух векторов,
- любая ось, и потому, согласно критерию равенства двух векторов,
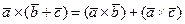 .
.
4. 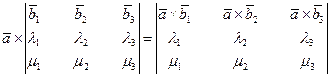 .
.
Доказательство. Воспользуемся равенством:
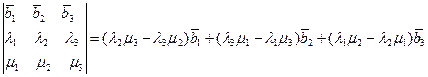 .
.
Тогда, в силу свойств 2 и 3 векторного произведения двух векторов, имеем
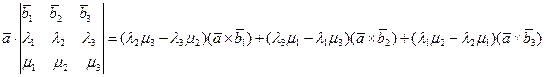
то есть
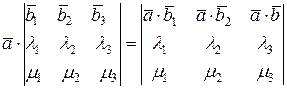 .
.
5. Векторное произведение вектора самого на себя есть нуль-вектор:
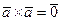 .
.
Доказательство. Справедливость этого утверждения с очевидностью следует из определения векторного произведения двух векторов.
6. Имеет место следующая таблица векторных произведений координатных ортов:
| Второй множитель | ||||
| Первый множитель | 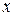
| 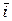
| 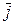
| 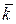
|
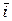
| 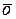
| 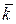
| 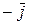
| |
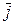
| 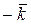
| 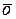
| 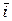
| |
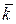
| 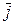
| 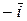
| 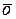
|
Справедливость этой таблицы следует из определения векторного произведения двух векторов.
7. Векторное произведение векторов  и
и  может быть представлено через проекции этих векторов на координатные оси по следующей формуле:
может быть представлено через проекции этих векторов на координатные оси по следующей формуле:
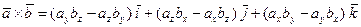
или, что то же самое,
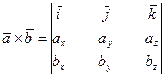 .
.
Доказательство. Разложим каждый из векторов  и
и  по координатным ортам:
по координатным ортам: 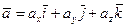 и
и 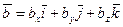 .
.
Воспользовавшись свойствами 2 и 3 векторного произведения двух векторов, имеем 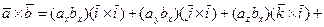
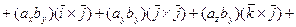
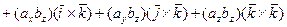 ,
,
или, с учетом таблицы векторных произведений координатных ортов,
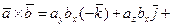
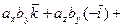
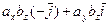 .
.
В силу свойств сочетательности и распределительности произведения вектора на скаляр, получим 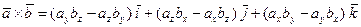 , или, что то же самое,
, или, что то же самое, 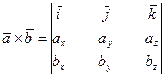 .
.
 2015-06-28
2015-06-28 450
450








