1. Основное свойство
Для двойного векторного произведения трёх векторов  ,
,  ,
,  справедливо равенство
справедливо равенство
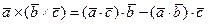 . (1)
. (1)
Доказательство. Проекции векторного произведения векторов  и
и  на координатные оси
на координатные оси 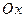 ,
, 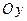 ,
, 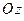 равны
равны
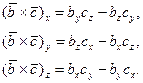 (2)
(2)
Для проекций векторного произведения векторов  и
и 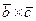 имеем
имеем
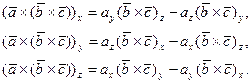 (3)
(3)
Чтобы убедиться в справедливости доказываемого равенства (1), достаточно показать, что
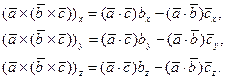
Действительно, согласно первого из равенств (3), 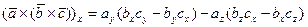 .
.
После тождественных преобразований (в правой части прибавим и вычтем 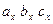 ) имеем
) имеем
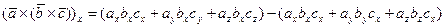
или, что то же самое,
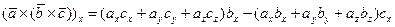
и, наконец, 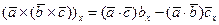
Аналогично доказывается справедливость равенств
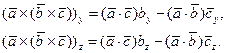
Следовательно,
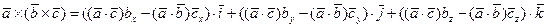
то есть
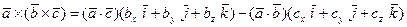 .
.
Таким образом, 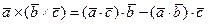 , что и требовалось доказать.
, что и требовалось доказать.
2. Для двойного векторного произведения трёх векторов справедливы равенства
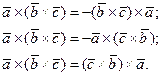
Доказательство. Равенства непосредственно следуют из свойств векторного произведения двух векторов.
3. Если векторы  и
и  коллинеарны, то
коллинеарны, то 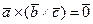 .
.
Доказательство. Для коллинеарных векторов  и
и  справедливо равенство
справедливо равенство 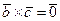 , откуда с очевидностью следует утверждение.
, откуда с очевидностью следует утверждение.
4. Если вектор  перпендикулярен векторам
перпендикулярен векторам  и
и  , то
, то 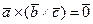
Доказательство. Для перпендикулярных векторов  ,
,  и соответственно
и соответственно  ,
,  имеем
имеем 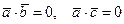 и потому, согласно формуле (1), действительно
и потому, согласно формуле (1), действительно 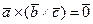 .
.
5. Если вектор  перпендикулярен вектору
перпендикулярен вектору  , то
, то 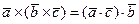 .
.
Доказательство. Так как векторы  и
и  перпендикулярны, то
перпендикулярны, то 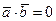 и, в силу формулы (1), убеждаемся в справедливости утверждения.
и, в силу формулы (1), убеждаемся в справедливости утверждения.
6. Если вектор  перпендикулярен вектору
перпендикулярен вектору  , то
, то  .
.
Доказательство. Так как векторы  и
и  перпендикулярны, то
перпендикулярны, то 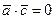 и, в силу формулы (1), убеждаемся в справедливости утверждения.
и, в силу формулы (1), убеждаемся в справедливости утверждения.
 2015-06-28
2015-06-28 659
659








