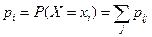 , (складываем по строкам), следовательно,
, (складываем по строкам), следовательно,
| xi | ||
| pi | 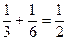
| 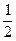
|
Проверка: 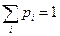 .
.
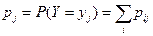 , (складываем по столбцам), следовательно,
, (складываем по столбцам), следовательно,
| yj | |||
| pj | 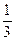
| 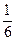
| 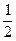
|
Проверка: 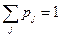 .
.
2. Функция распределения – закон распределения СВДТ и СВНТ.
Функция распределения – универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
Определение 5. Функцией распределения системы двух случайных величин называется функция двух аргументов F (x, y), равная вероятности совместного выполнения двух неравенств: X < x, Y < y, т.е.
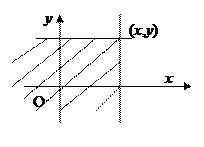 F (x, y) = Р (X < x, Y < y).
F (x, y) = Р (X < x, Y < y).
Геометрически F (x, y) представляет вероятность попадания случайной точки (X, Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (x, y).
F (x, y) = 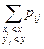 – для СВДТ
– для СВДТ
Свойства F(x, y).
1. Условие согласованности: F (x, +∞) = F 1(x), F (+∞, y) = F 2(y)
Пояснение. Отодвигая одну из границ квадранта в бесконечность, получаем полуплоскость, вероятность попадания в которую есть функция распределения одной случайной величины.

2. F (+∞, +∞) = 1
Пояснение. Квадрант обращается во всю координатную плоскость, попадание случайной точки в которую есть достоверное событие.
3. F (–∞, y) = F (х, –∞) = F (–∞, –∞) = 0
Пояснение. Отодвигая ту или иную границу квадранта в (–∞), убеждаемся, что вероятность случайной точки попасть в квадрант равна нулю.
4. F (x, y) – неубывающая функция по каждому аргументу.

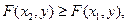 если х 2 > x 1,
если х 2 > x 1, 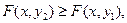 если y 2 > y 1.
если y 2 > y 1.
5. Вероятность попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
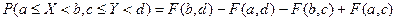
Определение 6. (второе определение) Двумерный случайный вектор называется случайным вектором непрерывного типа (СВНТ), если его функция распределения непрерывна на всей плоскости и существует неотрицательная и интегрируемая по Риману в бесконечных пределах по x, y функция f (x, y), называемая плотностью распределения СВНТ.
Пример 3. В примере № 1 п.2 найти функцию распределения, если случайный вектор задан таблицей распределения:
| xi \ yj | 2 | ||
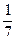
| |||
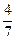
| |||
|
 2015-06-28
2015-06-28 505
505








