Вероятностный смысл двумерной плотности вероятностей

Из (3.6), определения производной и свойства 2F4) двумерной функции распределения получаем, что

.

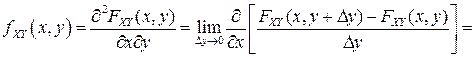
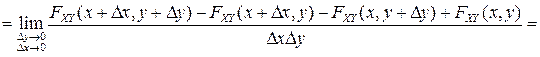
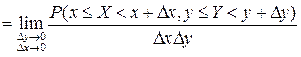Таким образом, плотность вероятностей 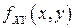- это предел отношения вероятности попадания непрерывного случайного вектора в прямоугольник со сторонам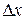и и 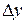, параллельными осям координат, к площади этого прямоугольника, когда длины обеих сторон стремятся к нулю (при интерпретации вероятности как массы, приходящейся на элементарный прямоугольник 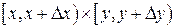, получаем, что 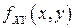есть плотность массы в точке ).

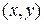При малых 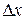и 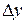можно также записать, что

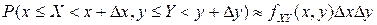. (3.7)