2015-06-28
809
nF0).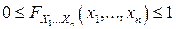 
для любых 
.
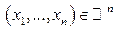nF1).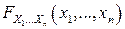 
является неубывающей функцией по каждому из своих аргументов.
nF2).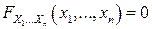 
, если хотя бы один из аргументов 
;
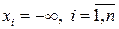по функции распределения 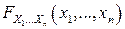случайного вектора 
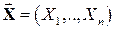можно найти функцию распределения любой совокупности 
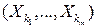из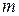 
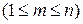его координат, для этого следует у функции распределения 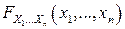положить аргументы 
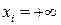для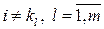 
(свойство согласованности);
.
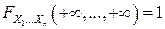nF3). 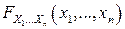является непрерывной слева функцией по каждому из своих аргументов.
Многомерный аналог свойства 2F4) двумерной функции распределения приводить не будем из-за необходимости введения разностных операторов и его громоздкой записи (подробности см. учебник Ширяева А.Н. «Вероятность»).
В приложениях, как правило, имеют дело со случайными векторами двух типов: дискретными и непрерывными. В каждом из этих случаев существуют более удобные, чем функция распределения, способы вероятностной характеристики случайных векторов.
