Непрерывные случайные векторы. Плотность вероятностей случайного вектора

Снова начнем с рассмотрения двумерного случайного вектора .

Определение. Случайный вектор , заданный на вероятностном пространстве 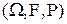, называется непрерывным (или имеющим непрерывный закон распределения), если существует такая функция 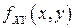, двух действительных переменных, что для любой точки 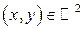функция распределения 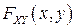случайного вектора допускает представление:

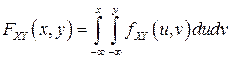. (3.5)

Функция 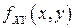при этом называется плотностью вероятностей случайного вектора или двумерной плотностью вероятностей или совместной плотностью вероятностей случайных величин и .

Из определения (3.5) следует:

1. Функция распределения 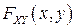непрерывного случайного вектора является непрерывно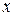й по и по 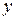(как двойной интеграл с переменными верхними пределами);

2. Функция распределения 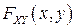непрерывного случайного вектора является дифференцируемо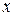й по и по 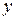во всех точках 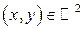, являющихся точками непрерывности двумерной плотности вероятностей 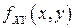, и при этом имеет место равенство:

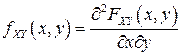(3.6)

(также по свойствам двойного интеграла с переменными верхними пределами).

Замечание. Другими словами (сравнить с соответствующим замечанием в разделе 2.4), равенство (3.6) справедливо почти всюду, кроме (возможно) 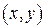из некоторого множества нулевой меры на плоскости (площади).