2f1). Двумерная плотность вероятностей 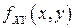 является функцией неотрицательной:
является функцией неотрицательной: 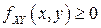 для любых
для любых 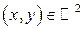 .
.
▲ Поскольку функция распределения 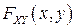 является неубывающей функцией по каждому из своих аргументов, то ее производная
является неубывающей функцией по каждому из своих аргументов, то ее производная 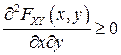 . Поэтому свойство следует из равенства (3.6) ■.
. Поэтому свойство следует из равенства (3.6) ■.
2f2). 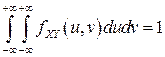 - условие нормировки.
- условие нормировки.
▲ Из представления (3.5) следует, что 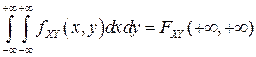 , а в соответствии со свойством 2F2) двумерной функции распределения
, а в соответствии со свойством 2F2) двумерной функции распределения 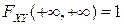 ■.
■.
2f3). Вероятность попадания непрерывного случайного вектора  в любое борелевское множество
в любое борелевское множество 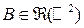 определяется формулой:
определяется формулой:
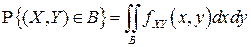 .
.
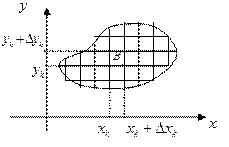 ▲ Разобъем множество
▲ Разобъем множество 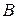 на
на 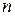
элементарных непересекающихся
прямоугольников 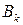 со сторонами,
со сторонами,
параллельными осям координат и
равными 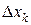 и
и 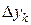 ,
, 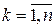 .
.
Так как в соответствии с (3.7) 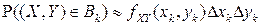 и
и 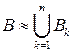 , то в силу аддитивности вероятности имеем:
, то в силу аддитивности вероятности имеем:
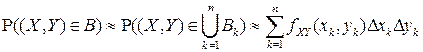 .
.
Последняя сумма является интегральной, и поэтому предельный переход при 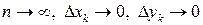 приводит к равенству
приводит к равенству
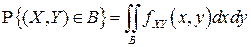 ■.
■.
Замечание. Приведенное доказательство свойства 2f3), хотя и не является полностью строгим, но обладает наглядностью и фактически основано на том, что любое борелевское множество 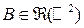 представимо в виде суммы элементарных прямоугольников.
представимо в виде суммы элементарных прямоугольников.
2f4). Координаты непрерывного случайного вектора  с плотностью вероятностей
с плотностью вероятностей 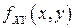 являются непрерывными случайными величинами, плотности вероятностей которых
являются непрерывными случайными величинами, плотности вероятностей которых 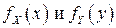 (маргинальные плотности вероятностей), выражаются через
(маргинальные плотности вероятностей), выражаются через 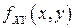 по формулам:
по формулам:
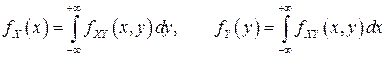 , (3.8)
, (3.8)
в точках непрерывности функций 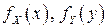 и
и 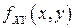 .
.
▲ Из представления (3.5) следует, что
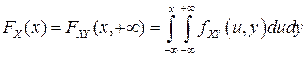 .
.
Дифференцируя обе части этого равенства по 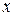 , в точках непрерывности функций
, в точках непрерывности функций 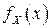 и
и 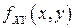 получаем:
получаем:
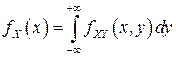 .
.
Аналогично, из представления (3.5)
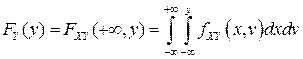
и после дифференцирования обеих частей последнего равенства по 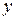 , имеем:
, имеем:
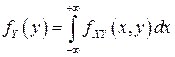
в точках непрерывности функций 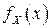 и
и 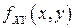 ■.
■.
Пример (Равномерное распределение в области 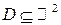 ).
).
Говорят, что непрерывный случайный вектор  имеет равномерное распределение в области
имеет равномерное распределение в области 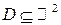 , если его плотность вероятностей постоянна внутри области
, если его плотность вероятностей постоянна внутри области 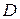 :
:
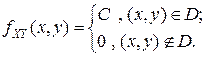
Константа С при этом однозначно определяется из условия нормировки:
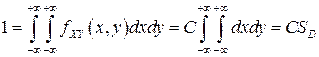 , то есть
, то есть 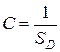 ,
,
где 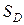 - площадь области
- площадь области 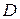 .
.
а) Равномерное распределение в прямоугольнике.
Непрерывный случайный вектор  имеет равномерное распределение в прямоугольнике
имеет равномерное распределение в прямоугольнике 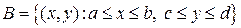 со сторонами, параллельными осям координат, если его плотность вероятностей имеет вид:
со сторонами, параллельными осям координат, если его плотность вероятностей имеет вид:
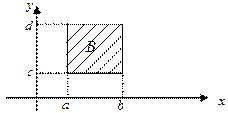
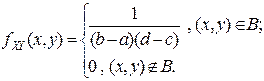
Найдем одномерные плотности вероятностей координат 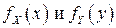 .
.
В соответствии со свойством 2f4) двумерной плотности вероятностей имеем (см. (3.8)):
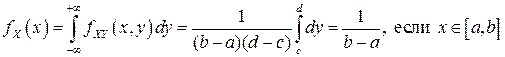 .
.
Таким образом, 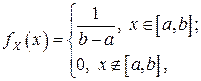 то есть
то есть 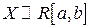 .
.
Аналогично, в соответствии с (3.8)
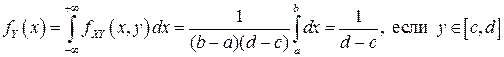 .
.
Таким образом, 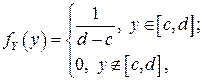 то есть
то есть 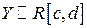 .
.
б) Равномерное распределение в круге.
 Непрерывный случайный вектор
Непрерывный случайный вектор  имеет равномерное распределение в круге
имеет равномерное распределение в круге 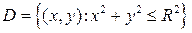 , если его плотность вероятностей имеет вид:
, если его плотность вероятностей имеет вид:
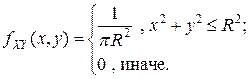
Найдем одномерные плотности вероятностей координат 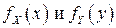 .
.
В соответствии со свойством 2f4) двумерной плотности вероятностей имеем (см. (3.8)):
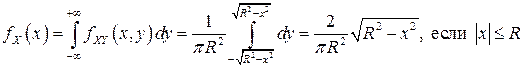 .
.
Таким образом, 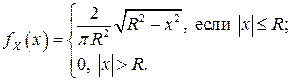
Аналогично, в соответствии с (3.8)
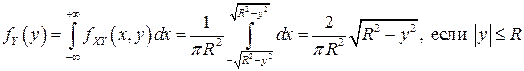 .
.
Таким образом, 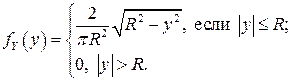
Все приведенные выше определения и формулы для двумерного непрерывного случайного вектора  легко обобщаются на случай
легко обобщаются на случай
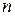 -мерного случайного вектора
-мерного случайного вектора 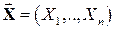 .
.
Определение. Случайный вектор 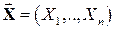 называется непрерывным, если существует такая функция
называется непрерывным, если существует такая функция 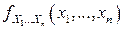
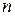 действительных переменных, что для любой точки
действительных переменных, что для любой точки 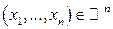 функция распределения
функция распределения 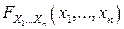 случайного вектора
случайного вектора 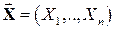 допускает представление:
допускает представление:

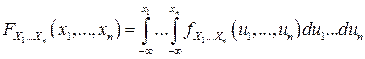 .
.
Функция 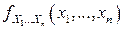 при этом называется плотностью вероятностейслучайного вектора
при этом называется плотностью вероятностейслучайного вектора 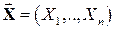 или многомерной (
или многомерной (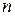 -мерной) плотностью вероятностей, или совместной плотностью вероятностей случайных величин
-мерной) плотностью вероятностей, или совместной плотностью вероятностей случайных величин 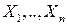 .
.
Во всех точках 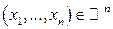 , являющихся точками непрерывности плотности вероятностей
, являющихся точками непрерывности плотности вероятностей 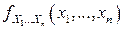 , имеет место равенство:
, имеет место равенство:
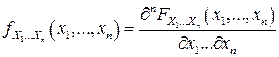 .
.
 2015-06-28
2015-06-28 1775
1775
