Определение взаимной ориентации векторов  ,
,  и
и  основано на следующих соображениях. Если
основано на следующих соображениях. Если 

 > 0, то
> 0, то  ,
,  ,
,  — правая тройка; если
— правая тройка; если 

 < 0, то
< 0, то  ,
,  ,
,  - левая тройка.
- левая тройка.
Установление компланарности векторов
Векторы  ,
,  ,
,  компланарны тогда и только тогда, когда их смешанное произведение равно нулю (
компланарны тогда и только тогда, когда их смешанное произведение равно нулю (  ≠ 0,
≠ 0,  ≠ 0,
≠ 0,  ≠ 0):
≠ 0):
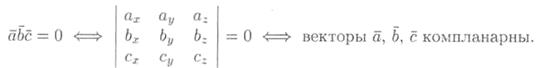
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах  ,
,  и
и  вычисляется как V = |
вычисляется как V = | 

 |, а объем треугольной пирамиды, построенной на этих же векторах, равен V = 1/6 |
|, а объем треугольной пирамиды, построенной на этих же векторах, равен V = 1/6 | 

 |.
|.
Пример 1. Вершинами пирамиды служат точки А(1; 2; 3), В (0; -1; 1), С (2;5;2) и D (3;0; -2). Найти объем пирамиды.
Решение: Находим векторы  ,
,  ,
,  :
:
 =
= 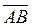 =(-l;-3;-2),
=(-l;-3;-2),  =
= 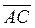 = (1;3;-1),
= (1;3;-1),  =-
=- 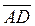 = (2; -2; -5).
= (2; -2; -5).
Находим 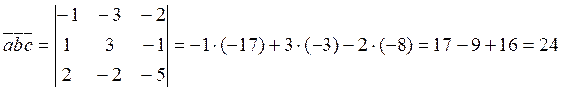
Следовательно, 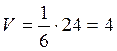
 2015-06-28
2015-06-28 2479
2479







