Векторы

Векторы и тензоры в ортогонaльных координатах.

1. Векторы.

2. Линейное преобразование векторов.

3.Тензоры.

4. Поворот системы координат.

5. Преобразование компонентов векторов при повороте осей координат.

6.Преобразование компонентов тензора при повороте осей координат.

7.Симметричные антисимметричные и ортогональные тензоры.

8. Главные оси и главные значения тензора.

9. Инварианты тензора.

10.Вырожденные и невырожденные тензоры.

11. О матрице поворота.

12. Скалярные произведения.

Векторы и тензоры в ортогонaльных координатах.

Векторы.

Пусть в трехмерном пространстве задан некоторый вектор a. В ортогональной (например, в декартовой) системе координат x₁,x₂,x₃ этот вектор будем характеризовать его компонентами – проекциями на координатные оси a₁,a₂,a₃, из которых скомпонуем матрицу-столбец (a) = (a₁,a₂,a₃)^T.

Длина вектора:

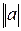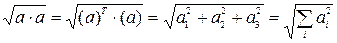= , i=1,2,3 (1)

Направляющие косинусы вектора:

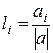(2)

Предполагается, что вектор a изображает существующий объект (например, скорость кокой-либо материальной точки, силу и т.п.). Объект, и следовательно, изображающий его вектор а не зависят от того, в какой системе координат мы их изучаем, тогда как компоненты вектора a_i, матрицa (a) и направляющие косинусы l_i зависят от системы координат, они меняются, например, при повороте координатной системы.

Можно построить такие комбинации из компонентов вектора, которые при повороте системы координат не будут меняться. Их называют инвариантами. Например, инвариантом вектора является сумма квадратов его компонентов (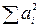), поскольку она равна квадрату длины вектора и от системы координат не зависит.

У вектора существует только один независимый инвариант.