Тензоры

В соотношениях (3) структуру, обозначенную b, можно рассматривать какнекоторый оператор, который осуществляет линейное преобразование вектора a в вектор b. Если эти векторы описывают объекты, существующие независимо от системы координат, выбранной для их описания, то и структура b существует независимо от системы координат. При этом, ее компоненты, то есть коэффициенты b_i,j, от системы координат зависят (как и компоненты векторов a_i и b_i).

Оператор, осуществляющий линейное преобразование вектора в вектор, называется тензором (2-ого ранга).

Таким образом, b - это тензор, b_i,j - его компоненты, (b) – его матрица в координатной системе x₁,x₂,x₃.

С использованием этого определения соотношение (3) можно записать в тензорно-векторной форме:

b = b×a (3т)

4. Поворот системы координат.

Введем новую ортогональную систему координат x₁^I, x₂ ^I, x₃^I, повернутую относительно старой x₁, x₂, x₃. Определим положение новой системы матрицей поворота (L), коэффициентами которой являются направляющие косинусы новых осей по отношению к старым:

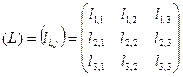
(4)

где l_i,j – косинус угла, который образует новая осью x_i^I со старой x_j.

5. Преобразование компонентов векторов при повороте осей координат.

Для того, чтобы определить компоненты вектора в новой координатной системе a_i^нов достаточно на ее оси спроецировать его компоненты в старой системе, умножая их на соответствующие направляющие косинусы. Для вектора a получится:

(a) ^нов = (L)·(a). (5)

или a_j^нов = L_j,I · a_i,

где (a)^нов =(a₁^н ,a₂^н ,a₃^н )^T - матрица-столбец, составленная из компонентов вектора a в новой координатной системе (суммиро-вание по повторяющимся индексам i и j),.

Аналогичным образом, проецируя компоненты вектора в новой системе на старые оси, можно построить обратное соотношение:

(a) = (L)^T·(a) ^нов, (6)

или a_j = L_i,ja_i^н

С другой стороны, его же можно получить, обратив соотношение (5):

(a) = (L^-1) ·(a) ^нов. (6a)

Таким образом, обратная матрица поворота равна транспонированной:

(L^-1) = (L^T). (7)

Если обратная матрица равна транспонированной, то матрица и соответствующий ей тензор называются ортогональными.

Матрица поворота (L) ортогональна.

6. Преобразованиекомпонентов тензора при повороте осей координат.

Пусть тензор b связывает векторы a и b соотношениями (3) в старых координатах. В новой координатной системе эти векторы связаны аналогичным соотношением:

(b)^нов = (b)^нов · (a)^нов , (8)

где – (b)^нов матрица компонентов тензора b в новых координатах.

Для того, чтобы установить правило преобразования компонентов тензора при повороте системы координат, применим к матрице (b)^нов соотношение (5), а затем выразим (b) через (a), используя (3d):

(b)^нов = (L)·(b) = (L)·(b)· (a).

Последний сомножитель формулы преобразуем, выразив старые компоненты вектора (a) через новые по формуле (6-а). Получим:

(b)^нов = (L) · (b) · (L^T) · (a) ^нов

Сравнивая результат с (8), получим уравнение, связывающее компоненты тензора b в новой и старой системах координат:

(b)^нов = (L) · (b) · (L^T) (9).