Линейной комбинацией векторов 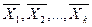 с коэффициентами
с коэффициентами 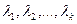 называется вектор
называется вектор 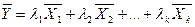 , в этом случае говорят так же, что вектор
, в этом случае говорят так же, что вектор 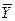 разложен по системе векторов
разложен по системе векторов 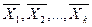 , а числа
, а числа 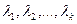 являются коэффициентами разложения.
являются коэффициентами разложения.
Пример 1. Дана система векторов
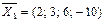 ,
, 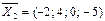 ,
, 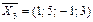
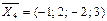 .
.
Найти линейную комбинацию: 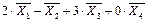 .
.
Решение. 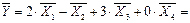 2·(2; 3; 6; -10)-(-2; 4; 0; -5)+3·(1; 5; -1; 3)+0·(-1; 2; -2; 3)=(4; 6; 12; -20)-(-2; 4; 0; -5)+(3; 15; -3; 9)+(0; 0; 0; 0)=(4+2+3+0; 6-4+15+0; 12-0-3+0; -20+5+9+0)=(9; 17; 9; -6)
2·(2; 3; 6; -10)-(-2; 4; 0; -5)+3·(1; 5; -1; 3)+0·(-1; 2; -2; 3)=(4; 6; 12; -20)-(-2; 4; 0; -5)+(3; 15; -3; 9)+(0; 0; 0; 0)=(4+2+3+0; 6-4+15+0; 12-0-3+0; -20+5+9+0)=(9; 17; 9; -6)
Вектор 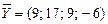 разлагается по системе векторов
разлагается по системе векторов 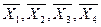 , и коэффициентами разложения являются числа: λ1=2; λ2=-1; λ3=3; λ4=0.
, и коэффициентами разложения являются числа: λ1=2; λ2=-1; λ3=3; λ4=0.
С помощью векторов удобно записывать систему уравнений:
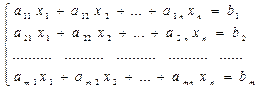
Введем в рассмотрение векторы-столбцы:
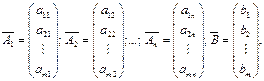
Тогда систему можно записать так:
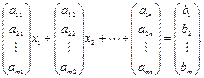
или 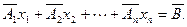
Если совокупность чисел 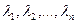 является решением системы (1.2), то вектор
является решением системы (1.2), то вектор 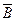 разлагается по векторам
разлагается по векторам 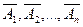 , и коэффициентами разложения являются числа
, и коэффициентами разложения являются числа 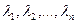 , т.е. справедливо соотношение:
, т.е. справедливо соотношение: 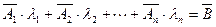 .
.
Таким образом, чтобы найти разложение вектора 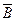 по системе векторов
по системе векторов 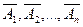 достаточно найти любое решение системы уравнений:
достаточно найти любое решение системы уравнений: 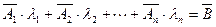 .
.
 2015-06-28
2015-06-28 2145
2145
