Наибольшее число r линейно-независимых векторов данной системы (n-мерного пространства) называется рангом данной системы векторов (n-мерного пространства).
Базисом системы векторов, имеющей ранг r, называется любая группа из r линейно-независимых векторов данной системы.
Базисом n-мерного пространства является любая система из n линейно-независимых векторов. Базисов в n-мерном пространстве бесчисленное множество, один из них система из n n-мерных ортов:
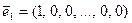

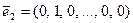
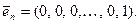
Такой базис называется единичным. 
Теорема: Если набор 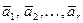 линейно-независимых векторов является базисом некоторого множества векторов, то любой вектор
линейно-независимых векторов является базисом некоторого множества векторов, то любой вектор 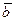 этого множества можно представить линейной комбинацией базисных векторов:
этого множества можно представить линейной комбинацией базисных векторов:
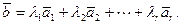
Такое представление называется разложением вектора 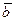 по базису
по базису 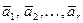 , коэффициенты
, коэффициенты 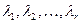 разложения определяются для данного вектора
разложения определяются для данного вектора 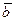 однозначно.
однозначно.
Пример: Дана система векторов 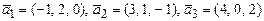 и
и 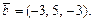
Показать, что векторы 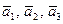 образуют базис трехмерного пространства и найти разложение вектора
образуют базис трехмерного пространства и найти разложение вектора 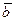 в этом базисе.
в этом базисе.
Найдем решение системы уравнений: 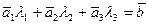
(-1; 2; 0)λ1+(3; 1; -1)λ2+(4; 0; 2)λ3=(-3; 5; -3). 
Решив систему получили единственное решение системы уравнений: 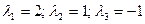 , подставляя в которое получаем разложение вектора
, подставляя в которое получаем разложение вектора 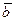 по базису, который образуют векторы
по базису, который образуют векторы 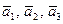 :
: 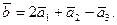
 2015-06-28
2015-06-28 872
872








