2015-06-28
955
Система векторов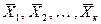 
называется линейно-зависимой, если можно подобрать такие числа 
, 
,..., 
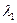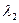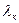не все равные нулю (есть 
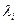≠0), что
(
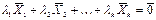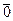- нуль-вектор)
Система векторов называется линейно-независимой, если из данных векторов нельзя составить нулевую линейную комбинацию с отличными от нуля коэффициентами, т.е. для линейно-независимой системы векторов выражение (1.3) справедливо тогда, когда все коэффициенты 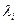=0,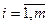 
.
Справедливы следующие утверждения.
Лемма. Если часть системы векторов линейно-зависима, то и вся система векторов линейно-зависима.
Теорема 1. Если система векторов линейно-зависима, то хотя бы один из них можно представить в виде линейной комбинации остальных векторов.
Следствие 1. Если хотя бы один вектор системы линейно выражается через остальные векторы, то система линейно-зависима.
Следствие 2. В линейно-независимой системе ни один из векторов нельзя выразить через остальные.
Теорема 2: Если каждый из векторов системы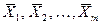 
линейно выражается через векторы 
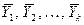(k<m), то система векторов 
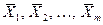линейно зависима.
Теорема 3: В n-мерном пространстве любая система, содержащая более чем n векторов линейно - зависима.
Следствие: В n-мерном пространстве любая линейно – зависимая система может содержать не более n векторов.
Таким образом, на плоскости линейно – независимыми могут быть только два вектора. Любой третий вектор можно представить линейной комбинацией этих двух векторов. В 3-х мерном пространстве линейно - независимыми могут быть не более трёх векторов и т.д.
Пример: Является ли система векторов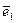 
= (1;0;0); 
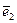= (0;1;0) и 
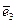= (0;0;1) линейно зависимой?
Решение: Составляем нулевую линейную комбинацию:
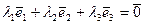
(1;0;0)λ1 + (0;1;0)λ2 + (0;0;1)λ3 =(0;0;0)
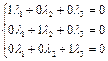или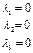 
Все значения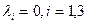 
, следовательно, система векторов 
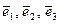– линейно – независима. Очевидно, что система из n n-мерных ортов является линейно-независимой.
