| Число редких | Среднее число редких событий (х) | ||||||
| событий (/я) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 1,0 | 1,5 | 2,0 |
| ООП | ||||||||
Примечание. В таблице нуль целых и запятая опущены.
Когда известны х и т, то по таблице 15 находим, что при х = = 0,4 и т = 3 вероятность появления трех уродов Ртз = 0,0072. Вероятность появления двух уродов — Ртг = 0,0536, одного — Ргщ = 0,2681 и отсутствие уродов — Рто = 0,6703.
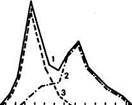
Трансгрессивные рады. Они характеризуются тем, что две или несколько кривых вариационных рядов лежат не отдельно, а заходят в большей или меньшей части друг на друга. Если два трансгрессивных ряда объединить и построить вариационную кривую, то обычно образуется двухвершинная кривая (рис. 33). В данном примере она указывает на то, что бурые латвийские и джерсейские помесные коровы различаются по содержанию жира в молоке, но часть животных имеет одинаковую жирномолочность.
Бывают случаи, когда сильно различающиеся трансгрессивные ряды не обнаруживают двухвершинности. Чем больше трансгрессия, тем более сходны два вариационных ряда. Если
|
Рис. 33. Двухвершинная кривая распределения по содержанию жира в молоке коров одного хозяйства, построенная без учета их породы, и кривые распределения по каждой из двух пород в отдельности (по О. А. Ивановой, 1974):
/ — по всему стаду; 2 — помеси с джерсейской породой; 3 — коровы бурой латвийской породы
| 3,4 3,6 4,0 4,6 5,0 5,4 5,8 ЖИРНОСТЬ МОЛОКА, % |
трансгрессия отсутствует, то кривые не соприкасаются друг с другом.
При изучении изменчивости нельзя объединять в одну группу животных разных пород, неодинакового возраста, выращенных в различных условиях среды и т. д.
КРИТЕРИЙ ХИ-КВАДРАТ (у2)
При анализе результатов скрещивания организмов исследователь почти всегда сталкивается с положением, когда фактическое расщепление в большей или меньшей степени отличается от теоретически ожидаемого. Поэтому возникает необходимость оценить степень соответствия фактических данных теоретически ожидаемым. Это достигается путем вычисления критерия соответствия х2 и сравнением полученной величины с табличным значением (с учетом числа степеней свободы). Критерий х2 является положительной величиной и изменяется от нуля до бесконечности. Если х2 = 0) то наблюдается полное соответствие фактического расщепления теоретически ожидаемому. С увеличением разности между эмпирическими и теоретическими частотами возрастает величина х2, и при превышении определенного табличного значения различия, между фактическим и теоретическим расщеплением будут достоверными. При сравнении достоверности разности между двумя и более группами для изучения влияния определенных факторов в изменчивости признаков наряду с дисперсионным и другими методами применяется и более простой критерий хи-квадрат. Критерий х2 также используют для изучения связи между признаками (особенно имеющими качественные градации). Однако х2 указывает не на степень связи, а только на ее наличие или отсутствие. Критерий х2 вычисляют по формуле
..?. V (О~Е)2
 где О — фактически наблюдаемая величина; Е — теоретически (гипотетически) ожидаемая величина.
где О — фактически наблюдаемая величина; Е — теоретически (гипотетически) ожидаемая величина.
Число степеней свободы при использовании хи-квадрата. При
оценке нормального и биномиального распределения из числа

 классов вариационного ряда вычитается 2 или 3. Если фактическое итеоретическое распределение совпадают но двум параметрам (х и л), то v = л — 2, а если по трем (х, я, а), то v = л — 3. При четырех (2 х 2) и многопольных таблицах (2 х 3, 2 х 4 и т. д.) используют формулу
классов вариационного ряда вычитается 2 или 3. Если фактическое итеоретическое распределение совпадают но двум параметрам (х и л), то v = л — 2, а если по трем (х, я, а), то v = л — 3. При четырех (2 х 2) и многопольных таблицах (2 х 3, 2 х 4 и т. д.) используют формулу
где г — число горизонтальных строк; с — число вертикальных столбцов.
При распределении Пуассона v = п — 2. При изучении полиморфизма белков число степеней свободы равно числу феноти-пических классов минус число аллелей. При скрещиваниях число степеней свободы равно числу фенотипических классов минус единица. Так, если расщепление по фенотипу 3: 1 или 9:7, TOV — 2 — 1 = 1, если расщепление 1:2:1, tov = 3 — 1 = 2, при расщеплении 9:3:3:1 v = 4 — 1 = 3.
Определим степень соответствия фактического распределения семейств по количеству больных туберкулезом коров теоретически ожидаемому, которое было вычислено при рассмотрении биномиального распределения. Данные приведены в таблице 16.
 2015-06-28
2015-06-28 492
492








