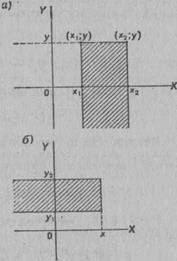
 Используя функцию распределения системы случайных величин X и Y, легко найти вероятность того, что в результате испытания случайная точка попадает в полуполосу
Используя функцию распределения системы случайных величин X и Y, легко найти вероятность того, что в результате испытания случайная точка попадает в полуполосу 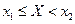 и Y < y (рис. 1, а) или в полуполосу
и Y < y (рис. 1, а) или в полуполосу
Х < x и 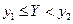 (рис. 1,б).
(рис. 1,б).
Вычитая из вероятности попадания случайной точки в квадрант с вершиной 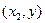 вероятность попадания точки в квадрант с вершиной
вероятность попадания точки в квадрант с вершиной 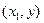 (рис. 1, а), получим
(рис. 1, а), получим
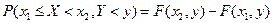
Аналогично имеем
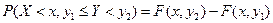
Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
Рассмотрим прямоугольник ABCD со сторонами, параллельными координатным осям. Пусть уравнения сторон таковы: 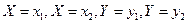
Вероятность попадания случайной точки (X; У) в этот прямоугольник равна
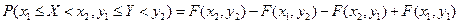 .
.
 2015-06-28
2015-06-28 2556
2556
