Классическое определение вероятности
В предыдущих примерах мы определяли вероятности событий, основываясь на интуитивном понятии равновозможности всех мыслимых исходов данного эксперимента. Эту схему можно распространять на случай любого конечного пространства равновозможных элементарных событий.
Действительно, пусть имеется вероятностное пространство 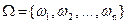 , состоящее из n равновозможных исходов
, состоящее из n равновозможных исходов 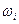 :
:
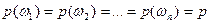
 .
.
Тогда в силу определения вероятности имеем 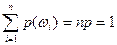 , откуда получаем
, откуда получаем 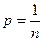 . Следовательно, вероятность события А, состоящего из m исходов, будет равна
. Следовательно, вероятность события А, состоящего из m исходов, будет равна
P (A) =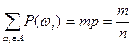 . (1)
. (1)
т.е. вероятность события А равна отношению числа исходов, благоприятствующих этому событию, к общему числу исходов, если все исходы равновозможны.
Пример. В двух урнах находятся белые и черные шары, причем в одной из них находится 6 белых и 10 черных, а в другой – 12 белых и 6 черных шаров. Из обеих урн наугад извлекаются по одному шару. Найти вероятности следующих событий:
А ={оба шара белые}; В ={оба шара черные}; С ={один шар белый, а другой черный}.
Пространство элементарных событий  , соответствующее данному эксперименту, состоит из всевозможных пар (k, l), где k =1,....16, l =1,…18. Общее число таких пар равно kl = 16∙18=288. Количество пар, благоприятствующих событиям А, В и С равны соответственно: mA=6∙12 = 72; mB=10∙6 = 60; mC = 6∙6+10∙12=156.
, соответствующее данному эксперименту, состоит из всевозможных пар (k, l), где k =1,....16, l =1,…18. Общее число таких пар равно kl = 16∙18=288. Количество пар, благоприятствующих событиям А, В и С равны соответственно: mA=6∙12 = 72; mB=10∙6 = 60; mC = 6∙6+10∙12=156.
Следовательно, согласно формуле (1) получаем: P (A) = 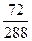 ; P (В) =
; P (В) = 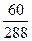 ;
;
P (С) = 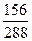 .
.
- Вероятность достоверного события равна 1.
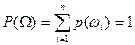 .
. - Вероятность суммы двух несовместных событий равна сумме их вероятностей.
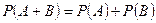 .
.
В самом деле, пусть 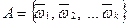 ,
, 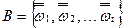 .
.
Так как 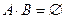 (или
(или 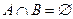 ), то
), то 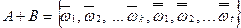 и, следовательно,
и, следовательно, 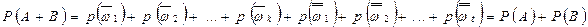 .
.
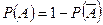 .
.
Действительно, т.к.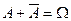 и
и 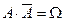 , то в силу предыдущего свойства
, то в силу предыдущего свойства 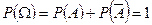 , откуда получаем требуемое.
, откуда получаем требуемое.- Если
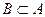 , то вероятность разности
, то вероятность разности 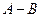 равна разности вероятностей:
равна разности вероятностей: 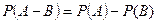
Действительно, если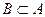 , то
, то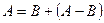 , причем
, причем 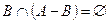 . Следовательно по теореме сложения вероятностей имеем
. Следовательно по теореме сложения вероятностей имеем 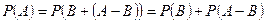
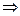
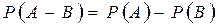 .
. - Для произвольных событий
 и
и 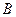 имеет место формула
имеет место формула 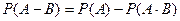 .
.
Так как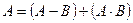 и события
и события 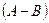 и
и 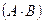 не пересекаются, то в силу теоремы сложения вероятностей
не пересекаются, то в силу теоремы сложения вероятностей 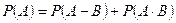 и, следовательно,
и, следовательно, 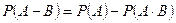 .
. - Для любых событий
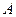 и
и 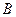 справедлива формула:
справедлива формула:
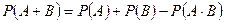 . (1)
. (1)
Поскольку 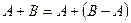 и события
и события  и
и 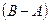 не пересекаются, то в силу свойств 2 и 5 имеем
не пересекаются, то в силу свойств 2 и 5 имеем 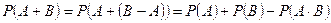 .
.
- Если
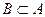 , то
, то 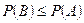 .
.
Это неравенство непосредственно вытекает из свойства 4.
- Для любых событий
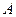 и
и 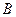 имеет место неравенство
имеет место неравенство 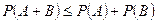
Данное соотношение сразу же следует из cвойства 6.
Заметим, что формула (1) обобщается на случай суммы любого конечного числа событий. Для простоты мы ограничимся лишь случаем суммы трех событий:
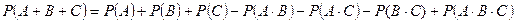 (2).
(2).
Аналогичная формула имеет место и для вероятности произведения трех событий:
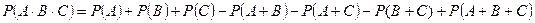
Пример1. Игральная кость подбрасывается три раза. Найти вероятность того, что хотя бы в одном испытании выпадет четное число очков.
Обозначим через 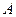 ,
, 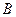 и
и 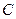 соответственно события.
соответственно события.
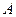 ={в первом испытании выпадет четное число очков};
={в первом испытании выпадет четное число очков};
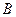 ={во втором испытании выпадет четное число очков};
={во втором испытании выпадет четное число очков};
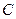 ={в третьем испытании выпадет четное число очков}.
={в третьем испытании выпадет четное число очков}.
Требуется найти вероятность события 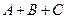 . Воспользуемся формулой (2). Так как
. Воспользуемся формулой (2). Так как
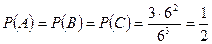 ,
,
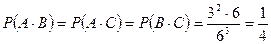 ,
,
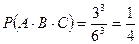 , то
, то 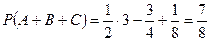 .
.
Пример 2. Три стрелка стреляют по мишени. Вероятность поражения мишени одним стрелком равна 0,6, другим 0,7 и третьим – 0,8. Какова вероятность поражения мишени тремя стрелками?
Обозначим 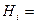 { i -й стрелок поразил мишень}, i =1, 2, 3.
{ i -й стрелок поразил мишень}, i =1, 2, 3.
Согласно формуле (2)
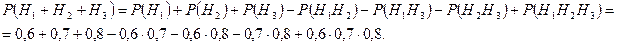
 2014-01-25
2014-01-25 721
721








