2015-06-24
1409
В основу школьного курса геометрии могут быть положены различные системы аксиом. Так, в учебниках, авторами которых являются А.Н. Колмогоров, А.В. Погорелов, Л.С. Атанасян и др., курс геометрии строится с помощью отличающихся друг от друга систем аксиом.
Определение [4.1]. Системы аксиом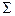 
и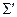 
называются эквивалентными, если в теории 
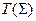, построенной с помощью системы аксиом 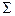, выполняются все аксиомы из 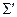и обратно: в теории 
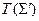, построенной с помощью системы аксиом 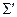, выполняются все аксиомы из .
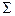Теорема [4.1]. Система аксиом Вейля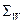 
пространства 
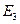эквивалентна системе аксиом 
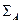школьного курса геометрии.
Лекция № _ 3 __.
Тема: ДЛИНА ОТРЕЗКА. ПЛОЩАДЬ МНОГОУГОЛЬНИКА _
Основные вопросы, рассматриваемые на лекции
1. Длина отрезка. Теорема существования и единственности. О единице измерения.
2. Определение площади многоугольника. Теорема существования и единственности.
3. Равновеликость и равносоставленность многоугольников.
