Свойства операций

n-местной операцией ω на множестве М называется функция ω: Мⁿ → М, или в другой записи ω = ω(<х₁,х₂,…,х_n>); x_i Î М, ω Î М. Компоненты кортежа <х₁,х₂,…,х_n> называют аргументами, а ω(х₁,х₂,…,х_n) – результатом операции.

Таким образом, операция является частным случаем функции; этот термин обычно применяется тогда, когда аргументы и значения функции принадлежат одному и тому же множеству.

0⁰. Нульарные операции. Это отображения М⁰→ М.

Особого смысла в М⁰ не наблюдается, но в силу определения |М⁰|=1 это есть одноэлементного множество, поэтому аргумент нульарной операции – один единственный и, следовательно, единственным будет и результат операции – некоторый элемент М. По-другому, это функция, не имеющая аргументов, т.е. константа – элемент М. Следовательно, нульарная операция означает (или отмечает) некоторый фиксированный элемент М. Нульарных операций может быть столько, сколько элементов в множестве.

Некоторые множества имеют элементы, обладающие особыми свойствами (например, 0 в N, пустое множество, и т.п.). Иногда бывает удобно считать, что такие выделенные элементы являются результатом действия нульарной операции.

1⁰. Унарные операции. Это отображения М → М.

· На конечном множестве можно задать nⁿ унарных операций.

· Любая действительная функция от одной действительной переменной является унарной операцией, то же справедливо для комплексных чисел.

· Дифференцирование.

· Операции симметрии в геометрии.

· Операция умножения вектора на число в векторном пространстве является унарной операцией:

λ: а → λ а.

В этом примере имеется столько операций, сколько элементов множестве {λ}. Этот пример отличается от предыдущих тем, что в унарной операции «задействованы» два, вообще говоря, разных множества.

Существует важный класс унарных операций, фактически характеризующий свойства множества (его симметрию), на котором эта операция определена. Таковы, например, операции зеркального отражения в пространстве дополнения А → Ā в теории множеств, комплексного сопряжения z → z* на C, и т.д.

Инволюцией называется операция *, обладающая свойством: "хÍМ, **х = х, т.е. двукратное применение инволюции приводит к тождеству.

Задать унарные операции φ: М → М можно разными способами, например:

Ø перечислением (a₁→b₁,…, a_n→b_n) или {<a₁,b₁>,…,<a_n, b_n>};

Ø двухстрочной матрицей перестановок 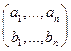, а если предварительно задан список (a₁,…,a_n) (т.е. элементы перенумерованы), то достаточно задать вектор значений: (b₁,…,b_n);

Ø аналитическим выражением типа φ(a)=b, например, ln(a)=b;

Ø алгоритмом и т.д..

2⁰. Бинарные операции. Это функции ◦: М ‰ М → М. Их принято записывать в инфиксной форме как ω = a◦b или как функцию ω(a,b). Употребляются также префиксная ◦(a,b) и постфиксная (a,b)◦ формы записи.

Для задания бинарных отношений часто используются так называемые таблицы Кэли, представляющие собой квадратные матрицы, по горизонтали и вертикали которых перечисляются элементы множества М, а на пересечении пишется результат операции.

Операция ◦ называется:

1) ассоциативной, если (x◦y)◦z=x◦ (y◦z);

2) коммутативной, если x◦y=y◦x;

3) идемпотентной, если x◦x=x.

Если операция ассоциативна, то в формулах можно опустить скобки. Бинарными операциями являются сложение и умножение чисел, сложение векторов и матриц, векторное умножение векторов в 3- х мерном пространстве, умножение матриц. Все эти операции ассоциативны, умножение матриц и векторное произведение векторов – некоммутативны. Пример неассоциативной операции – теоретико-множественная разность \, а также обычное деление чисел: a:b. Идемпотентны операции пересечения и объединения в теории множеств.

Пример

Пусть М= {0,1,2}. Определим операции сложения умножение на этом множестве следующими таблицами:

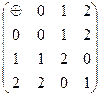
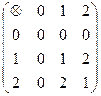
Непосредственно проверяются свойства ассоциативности и коммутативности операций, существование нуля и единицы, а также дистрибутивности (одной!). Набор (M; Å,Ä) называется алгеброй чисел по mod(3); более точно полем, или полем Галуа.

3⁰. Элемент «0» называют левым (правы м) нулём относительно операции ◦, если 0◦x=0(x◦0=0) для всех элементов x.

Если существуют левый и правый нули, то они совпадают. Действительно 0_Л=0_Л◦0_П=0_П. Аналогично доказывается единственность лево-правого нуля. Если нуль «односторонний», то их может быть несколько.