Кантор

Рассмотрим множество всех последовательностей нулей и единиц, т.е. (а₁а₂ … а_n …), где а_r=0 или 1. Обозначим множество таких двоичных последовательностей через {0,1}^ω = B^ω.

Теорема Кантора. Множество {0,1}^ω не есть счётное множество.

Предположим противное, т.е. что множество {0,1}ω счётное. Тогда существует биекция ν: N →{ 0,1}^ω. Выпишем её:

ν(1)={a₁₁,a₁₂,…,a_1n,…}

ν(2)={a₂₁,a₂₂,…,a_1n,…}

………………………..

ν(n)={a_n1,a_n2,…,a_nn,…}

………………………

По данной таблице построим последовательность β={β₁, β₂,…, β_n…} таким образом, что β_i=ā_nn, т.е. каждый член последовательности не совпадает с диагональю таблицы, и, следовательно, не совпадает ни с одной последовательностью ν(n). – Это противоречит допущению, что любая последовательность из {0,1}^ω есть ν(n) для некоторого n.

В то же время {0,1}^ω содержит подмножество последовательностей, у которых только один член не равен нулю. Эта последовательность равномощна множеству натуральных чисел. Следовательно, {0,1}^ω бесконечно, но не равномощно N.

Теорема. Множество 2 ^N (булеан) всех подмножеств множества натуральных чисел и множество {0,1}^ω равномощны.

Множеству X = {n₁,n₂,…,n_k,…}Í N сопоставим последовательность φ(X) = (а₁а₂ … а_n …)Í {0,1}^ω по правилу: a_n =1, если nÎX, и a_n =0 в противном случае. Докажем, что это инъекция. Пусть X,YÍN и X ≠ Y. Тогда найдётся число iÎ X\Y или jÎY\X. В первом случае в последовательности φ(Х) i-ый член будет равен 1, а в φ (Y) – нулю. Во втором случае (φ(Y))_j = 1 и (φ(Y))_j = 0 и, следовательно, в обоих случаях φ(Y) ≠ φ(Х). Докажем, что это сюръекция. Пусть α Í 0,1}^ω. Образуем множество X_α = {n|α_n = 1}. Ясно, что φ(Х_α) = α.. Таким образом, для любой последовательности α 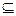{0,1}^ω существует подмножество X_α 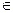2^N, такое, что φ(Х_α) = α.. Следовательно, φ – сюръекция.

Мощность множества {0,1}^ω обозначают с и называют мощностью континуума.

Теорема. Множество действительных чисел отрезка [0,1] имеет мощность континуума.

Доказательство – представление в виде дроби.

Примеры множеств мощности континуума.

Пока мы говорили о равенстве мощностей. Но, оказывается, можно сравнивать между собой и неравномощные множества.

Будем говорить, что мощность множества А не превышает мощности множества В, если A ≈ C и CÍB, т.е. А равномощно некоторому подмножеству В.

Обозначим: A´B

Мощность множества А строго меньше мощности множества В, если множества А и В неравномощны и существует собственное подмножество В, равномощное А:

ApB ÇА M В&A ≈ CÌB

Непосредственно проверяются свойства введённых отношений: (ир)рефлексивность, антисимметричность и транзитивность.

Следовательно, на множестве мощностей всех множеств установлены отношения порядка.

Из определения следует, что мощность любого конечного множества строго меньше א₀, а א₀ строго меньше с. Кроме того, согласно теореме мощность счётного множества является наименьшей из возможных мощностей безконечных множеств – начальная точка отсчёта.

Теорема. Если одновременно А´ В и В´ А, то А ≈ В.

Теорема Кантора-Бернштейна. Для любых двух множеств А и В имеет место в точности одно из трёх условий: либо Аp В, либо В p А, либо А ≈ В.

Теорема Кантора-Берштейна утверждает, что любые два множества можно сравнить по шкале мощностей. А это, в свою очередь, означает, что все множества линейно упорядочены по шкале мощностей.

Теорема о квадрате. Для любого бесконечного множества М |M|=|M×M| (М ≈ М²).

Доказательство для континуума – две дроби можно объединить в одну дробь, записывая цифры через одну.

Следствие (ещё раз) – множество рациональных чисел счётно.

Итак, в квадрате (а, значит, и в кубе, М³ и т.д.) столько элементов, сколько и в самом множестве.

Теорема (Кантор). Для любого множества А p 2^А – строго меньше!