Морфизмы

Алгебры с разными типами имеют, очевидно, существенно различное строение. Если же алгебры имеют одинаковый тип, то наличие в них сходства можно характеризовать с помощью понятий гомоморфизма и изоморфизма.

Пусть даны две алгебры А={A; φ₁,…, φ_n} и B={B; ψ₁,…, ψ_n} одинакового типа.

Гомоморфизмом f алгебры А в алгебру В называется отображение f: A→B такое, что

"i f (φ_i(a₁,…,a_k))=ψ_i(f(a₁),…,f(a_k)).

Схематически гомоморфизм (для бинарной алгебры) можно изобразить рисунком или диаграммой:

(*)

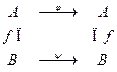Диаграмма гомоморфизма коммутативна: начиная с А, приходим в В по любому пути, т.е. результат не зависит от того, в какой последовательности применялись операции алгебры и отображение. Диаграмма называется коммутативной потому, что условие гомоморфизма (*) можно записать в виде: foj= yof, где o – суперпозиция функций.

Пример.

· Рассмотрим алгебры (¥; +,·) и (¥₇; Å,Ä) и определим отображение f₇: ¥→¥₇ следующим образом: f₇(n) равно остатку от деления n на 7. Это пример гомоморфизма бесконечной алгебры в конечную. При этом отображение f₇ разбивает ¥ на 7 классов эквивалентности по отношению «иметь одинаковый остаток от деления на 7».

· Гомоморфизмом является проекция линейного пространства на собственное подпространство.

Гомоморфизмы, обладающие дополнительными свойствами, имеют специальные названия.

ê Гомоморфизм, который является инъекцией, называется мономорфизмом.

ê Гомоморфизм, который является сюръекцией, называется эпиморфизмом.

ê Гомоморфизм, который является биекцией, называется изоморфизмом.

ê Если А = В, то гомоморфизм, называется эндоморфизмом, а изоморфизм – автоморфизмом.

· Пусть Q_2¥ – множество всех чётных чисел. Алгебры (¥; +) и (Q_2¥; +) изоморфны; изоморфизмом является отображение f: n→2n, причём условие гомоморфизма имеет здесь вид 2(a+b)=2a+2b. Отображение *: n→–n является для алгебры (¢; +) автоморфизмом, но это же отображение не является автоморфизмом для алгебры (¢; ·), поскольку (–a)(–b)≠–(ab).

· Изоморфизмом между алгебрами (¡₊; ·) и (¡;+) является отображение a→loga. Условие гомоморфизма имеет вид равенства logab=loga+logb.

· Булевы алгебры, образованные двумя различными множествами U и U′ одинаковой мощности, изоморфны: операции у них просто одинаковы, а отображением может служить любая биекция f.

· Алгебра (2^M,∩,Ç) изоморфна алгебре (2^M, Ç,∩), изоморфизм осуществляется отображением f(X)= X.

Лемма. Изоморфизм – это отношение эквивалентности на множестве однотипных алгебр.

Ø Рефлексивность: А ~ А при изоморфизме f=id_A.

Ø Симметричность: А ~ В → В ~ А; f→f^-1.

Ø Транзитивность: А ~ В & B ~ C→ А ~ C; h=f◦g.

Понятие изоморфизма является одним из центральных понятий, обеспечивающих применимость алгебраических методов в различных областях математики. Его существо можно выразить следующим образом: если алгебры A и B изоморфны, то элементы и операции B можно переименовать так, что B совпадёт с A.

Действительно, пусть A = (A, Σ_φ), B = (B, Σ_ψ) и A ~ B. Пусть в алгебре A установлено свойство Φ₁ = Φ₂, где Φ₁ и Φ₂ – некоторые формулы в сигнатуре Σ_φ. Поскольку алгебры изоморфны, отсюда немедленно следует, что в алгебре B справедливо свойство Ψ₁ = Ψ₂, где Ψ₁ и Ψ₂ – формулы в сигнатуре Σ_ψ, полученные из Φ₁ и Φ₂ заменой операций из сигнатуры Σ_φ на соответствующие операции из сигнатуры Σ_ψ. Таким образом, достаточно доказать какое-либо свойство в одной алгебре, и оно автоматически распространяется на все изоморфные алгебры.

Распространённое в математике выражение «рассматривать объекты с точностью до изоморфизма» означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, т.е. являются общими для всех изоморфных объектов. В частности, изоморфизм сохраняет ассоциативность, коммутативность и дистрибутивность.