Факторгруппа

1) Циклические группы C _n – группы с одной образующей. – Перечисление –

Изоморфизм группе корней из единице (мультипликативной) и группе сложения по модулю – аддитивной. Изоморфизм осуществляется логарифмом.

Таблица умножения.

Представление (регулярное) группы – матрицы вида

Следствие – матрицы данного вида имеют собственные значения, равные корням из единицы.

Рассмотрим группы небольших порядков.

Группа из двух элементов С₂. Перестановка элементов. Представление в виде матрицы. Реализация как двух единиц. Запись отрицательных чисел.

Группа из 3–х элементов – только циклическая (3 – простое число). Доказательство.

Две группы из 4–х элементов. 4 единицы – запись комплексных чисел в виде матриц.

Группа прямоугольника (ромба).

Группа из 5–ти элементов – Циклическая – доказать. Следствие – все группы до 5–го порядка – абелевы.

C_n = {e = a⁰, a, …, a^n–1}» <¢_n, Å_n>» { 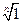} = {e^2pik/n}

Таблица умножения С₂: 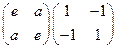. e(e,a) = (e,a); a(e,a) = (a,e) = (e,a) 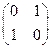. Получилось соответствие: 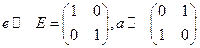– ещё одна реализация группы (а² = е). Рассмотрим объекты вида x₀e+ 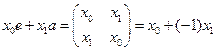– возможность описывать отрицательные числа.

Более интересна попытка описать комплексные числа. Результат – 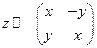– законы сложения и умножения комплексных чисел реализованы в матричной форме. Для получения такого представления следует исходить из группы С₂.

Группа С₃ может быть также реализована в матричном виде: 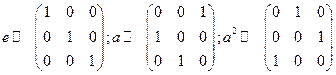. Следовательно (!), собственными значениями этих матриц являются корни 3–ей степени из единицы. Можно построить циклические числа вида 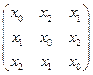или «комплексные» тернарные числа .

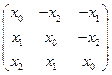2) Симметрическая группа S_n.

Представление элементов группы в виде двухстрочных матриц.

Построение групп с n = 3,4,5

Разбор группы D₃.

3) Групповые алгебры.

Рассмотренные построения являются реализациями весьма общей конструкции, называемой групповой алгеброй. Будем считать элементы группы G = {g₁, …, g_n} базисными векторами некоторого линейного пространства L. Элементами L являются (формальные) суммы вида 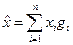, коэффициенты х являются элементами некоторого поля F. В поле F есть операции сложения и умножения на эти элементы. Таким образом, получается линейное пространство n измерений над группой, или «натянутое на группу», в котором, помимо линейных операций сложения и умножения в поле, определено действие группы: G: L a L по формуле 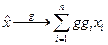. Таким образом, определено представление группы G на элементах линейного пространства L. Это представление называется регулярным представлением группы.

Помимо линейных операций, на L можно определить бинарную (билинейную) операцию умножения L´LaL формулой 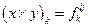, где справа стоит матрица из таблицы группового умножения.

Циклические и комплексные циклические числа получаются именно таким способом. К сожалению, умножение в алгебрах, построенных над циклическими группами, имеет делители нуля или сводится (изоморфизм!) к алгебре комплексных чисел.