В пункте А был изложен метод построения 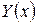 для специального вида
для специального вида 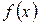 . Метод вариации произвольных постоянных применим для функции
. Метод вариации произвольных постоянных применим для функции 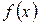 любого вида.
любого вида.
Итак, рассмотрим уравнение (1): 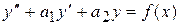 , где
, где 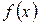 – любая функция (непрерывная).
– любая функция (непрерывная).
Пусть нам известно общее решение однородного уравнения (2)
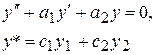 (7)
(7)
где 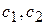 – произвольные постоянные, а
– произвольные постоянные, а 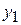 и
и 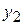 – частные решения уравнения (2).
– частные решения уравнения (2).
Будем искать частное решение уравнения (1) в виде 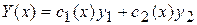 , (8)
, (8)
т.е. в таком же виде, как общее решение (7), но только вместо произвольных постоянных подставим пока неизвестные функции. Найдем их. Поскольку 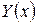 должно быть решением уравнения (1), то функции
должно быть решением уравнения (1), то функции 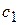 и
и 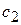 связаны только одной зависимостью. Для того чтобы их найти, этого недостаточно. Поэтому мы вправе наложить на них еще одно условие по произволу.
связаны только одной зависимостью. Для того чтобы их найти, этого недостаточно. Поэтому мы вправе наложить на них еще одно условие по произволу.
Найдем производную 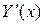 .
. 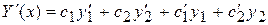 (9)
(9)
Потребуем, чтобы 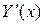 имело бы такой же вид, как если бы
имело бы такой же вид, как если бы 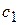 и
и 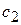 были бы постоянными. Отсюда следует, что должно быть
были бы постоянными. Отсюда следует, что должно быть
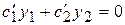 . (10)
. (10)
Тогда 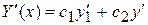 . (11)
. (11)
Найдем 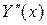 .
. 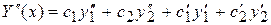 (12)
(12)
Подставляя 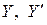 и
и 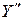 определенные формулами (9), (11) и (12), в уравнение (1), тогда получим:
определенные формулами (9), (11) и (12), в уравнение (1), тогда получим:
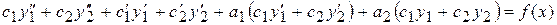
или 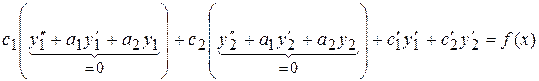 .
.
Но 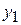 и
и 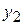 суть решения однородного уравнения (2), поэтому имеем
суть решения однородного уравнения (2), поэтому имеем
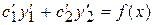 (13)
(13)
Таким образом, 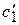 и
и 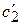 определяются из (10) и (13), т.е. из системы уравнений
определяются из (10) и (13), т.е. из системы уравнений
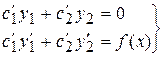 (14)
(14)
Эта неоднородная система линейных алгебраических уравнений относительно 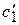 и
и 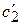 с определителем
с определителем 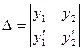 .
.
Это определитель Вронского, по доказанному ранее 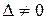 , поэтому система (14) имеет единственное решение. Определение из (14)
, поэтому система (14) имеет единственное решение. Определение из (14) 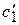 и
и 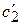 интегрируя их, найдем
интегрируя их, найдем 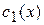 и
и 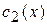 , а затем и
, а затем и 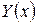 .
.
Замечание. Если при интегрировании 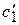 и
и 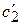 ввести произвольные постоянные, то сразу получим общий интеграл неоднородного уравнения (1).
ввести произвольные постоянные, то сразу получим общий интеграл неоднородного уравнения (1).
Пример. 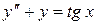
Соответствующее однородное 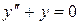
Характеристическое уравнение 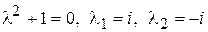 .
.
Общее решение однородного уравнения
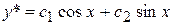
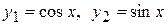
Частное решение заданного уравнения ищем в виде 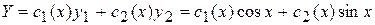 , где
, где 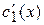 и
и 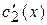 определяются из системы:
определяются из системы:
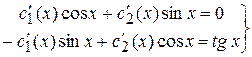
Отсюда 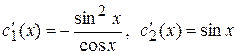
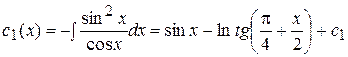
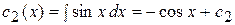
Общее решение будет
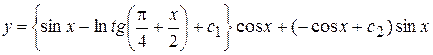
или 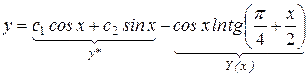 .
.
 2015-06-24
2015-06-24 418
418







